filmov
tv
Solving x^{1/ln(x)}=e^{x-1}

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #ExponentialEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
Solving x^{1/ln(x)}=e^{x-1}
Integral of e^x/x vs. integral of 1/ln(x)
Solve for x, e^(3x +1) = k, and ln x + ln(x-1) = 1. Natural exponential equations
Solve for x, ln(x+1)-(x+1)^(1/3)=0. A Nice Equation | The Lambert W function
Logarithmic Equations Solving : ln(x-1) + ln(2x-1) = 2ln(x+1)
OCR MEI Core 3 1.14 Solve ln(x + 1) + ln(x) = ln(6)
Solving an natural logarithmic equation using properties of logs
Is e^x=ln(x) solvable?
Integration in 15 Hours - Part 13
Solve for x, 1 less than e^(3x -1) less than 2 and , 1 - 2 ln x less than 3. Natural exponential
how is e^e^x=1 solvable??
How do you solve an exponential equation with e as the base
Solving x^{ln(x)}=ex
Why does e^(ln x) = x
Solving Exponential Equation
ONE OF THE COOLEST INTEGRALS EVER!!! int ln(x)/(1+e^x) from 0 to infty
The Exponential Function e and The Natural Log ln
Take the derivative of the natural log function
How to Find the Derivative of y = ln(e^x/(1 + e^x)) by using Properties of Logarithms First
Find the Inverse for an Exponential Rational Function
Solve for x ln(ln x) = 1, e^(e^x) = 10. Natural exponential functions
What is e and ln(x)? (Euler's Number and The Natural Logarithm)
ln(x^ln(x)) = (ln(x))^(ln(x)). Solving logarithm equation. How many real number answer for x?
Proof: Derivative of ln(x) = 1/x by First Principles
Комментарии
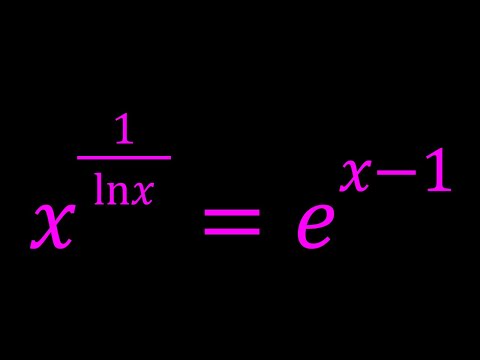 0:08:35
0:08:35
 0:08:48
0:08:48
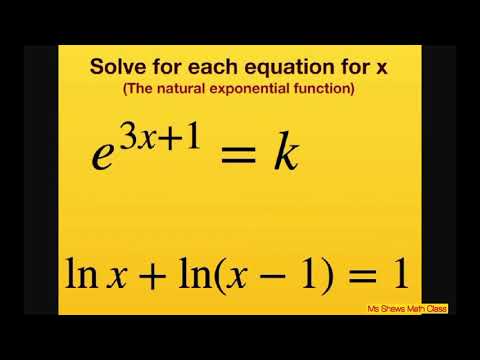 0:03:25
0:03:25
 0:05:59
0:05:59
 0:01:55
0:01:55
 0:01:35
0:01:35
 0:01:15
0:01:15
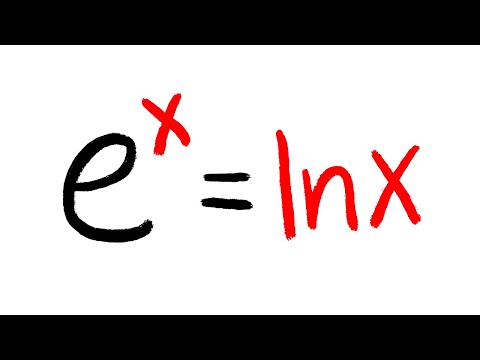 0:06:32
0:06:32
 1:03:22
1:03:22
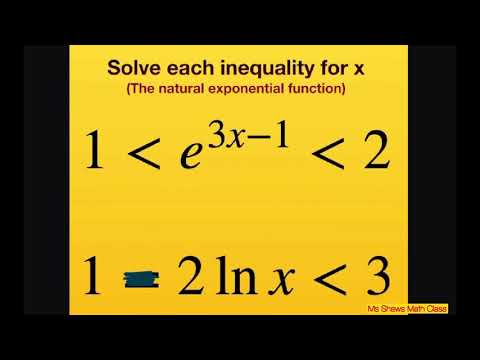 0:02:48
0:02:48
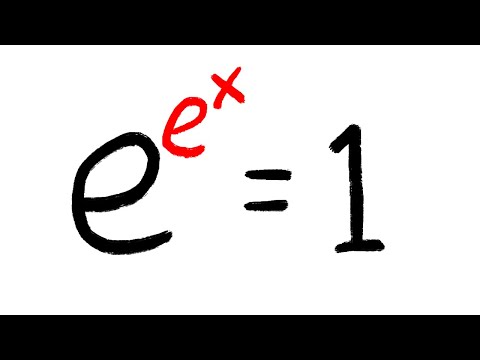 0:06:49
0:06:49
 0:02:47
0:02:47
 0:05:37
0:05:37
 0:02:05
0:02:05
 0:00:56
0:00:56
 0:19:24
0:19:24
 0:10:16
0:10:16
 0:00:43
0:00:43
 0:02:14
0:02:14
 0:03:45
0:03:45
 0:03:44
0:03:44
 0:12:02
0:12:02
 0:01:01
0:01:01
 0:08:14
0:08:14