filmov
tv
Machine Learning Lecture 14 '(Linear) Support Vector Machines' -Cornell CS4780 SP17
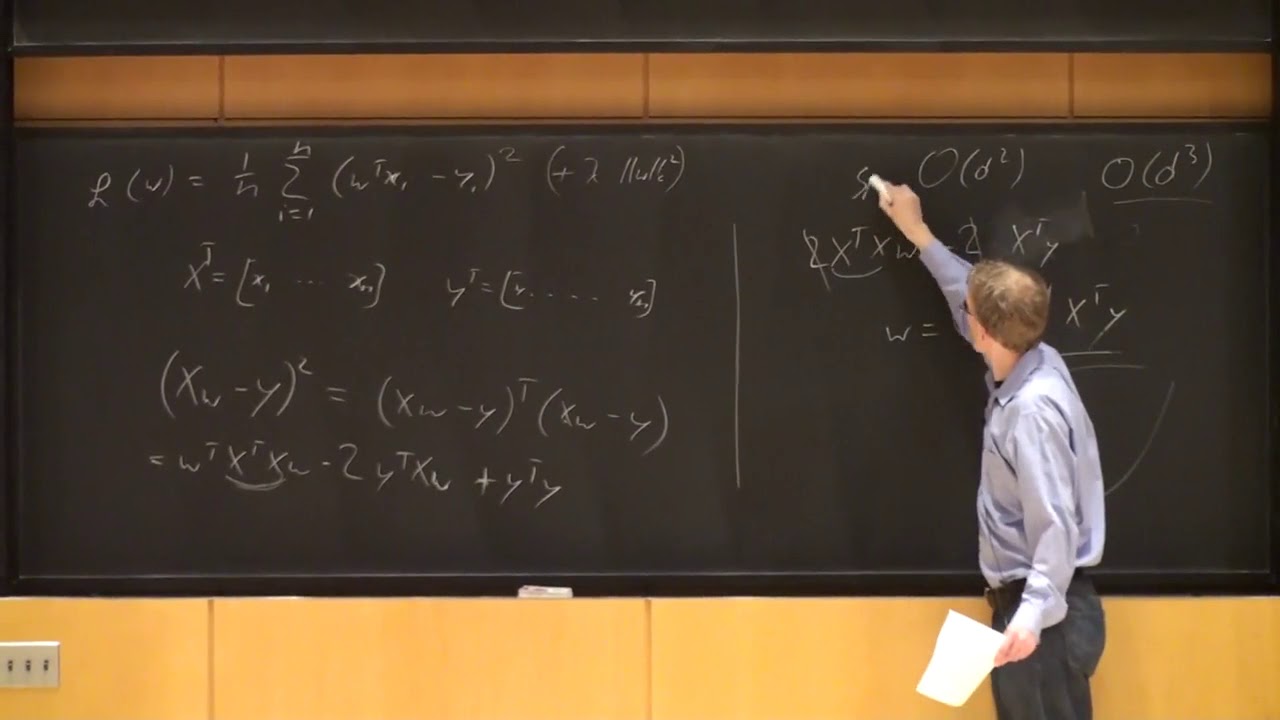
Показать описание
Lecture Notes:
Machine Learning Lecture 14 '(Linear) Support Vector Machines' -Cornell CS4780 SP17
Introduction to Machine Learning, Lecture-14( Applications of Linear Regression Model)
undergraduate machine learning 14: Linear algebra revision for machine learning and web search
MLAI Lecture 14: Univariate Bayesian Linear Regression
Machine Learning Lecture 15 '(Linear) Support Vector Machines continued' -Cornell CS4780 S...
Lecture 6: Linear Regression and Gradient Descent Optimization – Machine Learning for Engineers
14. Linear vs Nonlinear models
Lecture 14: Functional Linear Models
🔴Machine Learning Free Full Course 10 Hours
Linear Regression Algorithm – Solved Numerical Example in Machine Learning by Mahesh Huddar
Machine Learning Lecture 13 'Linear / Ridge Regression' -Cornell CS4780 SP17
Andrew Ng's Secret to Mastering Machine Learning - Part 1 #shorts
Eigenvectors and eigenvalues | Chapter 14, Essence of linear algebra
Lec-4: Linear Regression📈 with Real life examples & Calculations | Easiest Explanation
Machine Learning Lecture 35 'Neural Networks / Deep Learning' -Cornell CS4780 SP17
Stanford CS229: Machine Learning | Summer 2019 | Lecture 4 - Linear Regression
Machine Learning Foundations Course – Regression Analysis
Linear Regression Explained in Hindi ll Machine Learning Course
Bro’s hacking life 😭🤣
Lecture 14 | Applied Linear Algebra | Vector Properties | Prof AK Jagannatham
14. Causal Inference, Part 1
Artificial Intelligence & Machine learning 3 - Linear Classification | Stanford CS221 (Autumn 20...
Machine learning - Maximum likelihood and linear regression
IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit
Комментарии
 0:49:59
0:49:59
 0:20:26
0:20:26
 0:52:38
0:52:38
 0:47:35
0:47:35
 0:50:04
0:50:04
 1:43:16
1:43:16
 0:16:56
0:16:56
 0:25:46
0:25:46
 9:35:08
9:35:08
 0:05:30
0:05:30
 0:39:50
0:39:50
 0:00:48
0:00:48
 0:17:16
0:17:16
 0:11:01
0:11:01
 0:49:39
0:49:39
 1:48:00
1:48:00
 9:33:29
9:33:29
 0:14:20
0:14:20
 0:00:20
0:00:20
 0:34:07
0:34:07
 1:18:43
1:18:43
 0:28:02
0:28:02
 1:14:01
1:14:01
 0:00:12
0:00:12