Intro Complex Analysis, Lec 31, Laurent Series, Poles of Complex Functions, Essential Singularities

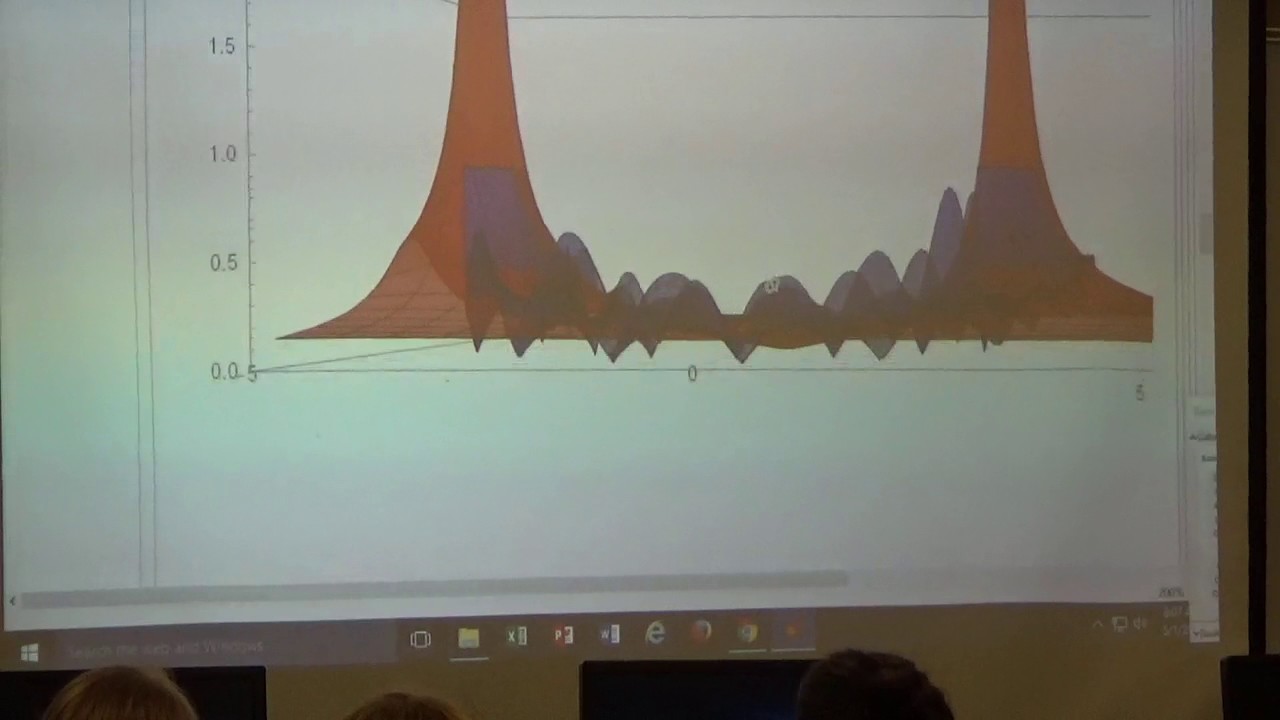
Lecture 31. (0:00) Exam 3 date change. (0:32) Review expansion and visualization of f(z) = z/(z^2 + z - 12) as a Laurent series in a disk centered at z = 0 and an annulus centered at z = 0. (11:20) Find the Laurent series centered at z = -4 (converging on a punctured disk of radius 7 centered at -4). (27:13) The pole at z = -4 has order 1. (27:59) A new example with a pole of order 2 at z = -4 (for f(z) = z/((z+4)^2*(z-3))). (34:52) What happens when you integrate over a contour around the pole of order 2? The only term that gives a nonzero integral is the (z + 4)^(-1) terms. Check the answer on Mathematica. (41:35) Find the Laurent series for (e^(z) - z)/z centered at z = 0. The function has a removable singularity there. The singularity can be "removed" by redefining the function at z = 0 (with a piecewise formula). (46:47) Find the Laurent expansion for e^(1/z) centered at z = 0. There are infinitely many negative powers of z in it. It has an essential singularity at z = 0. The behavior of this function near z = 0 is very strange (or "wild"). Use Mathematica to plot the level curves (contour map) for the real and imaginary parts of the function. Plot them both at the same time to see the orthogonal families of curve. The function ultimately attains every complex number output except 0 on any neighborhood of the origin, no matter how small. This type of thing happens for any function with an essential singularity. The behavior near an essential singularity is wild.

AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.