filmov
tv
Intro Complex Analysis, Lec 13, Preimages, Laplace's Equation, Harmonic and Analytic Functions

Показать описание
Lecture 13. (0:00) Topics for the lecture. (0:32) Level curves of the real and imaginary parts of a complex-valued function are preimages of horizontal and vertical lines under the mapping. (3:26) Symbolically confirm that hyperbolic functions parameterize hyperbolas. (6:33) Animate hyperbolas being mapped under f(z) = z^2. (12:13) Review Cauchy-Riemann equations in polar coordinates and check them for f(z) = z^3 in both rectangular and polar coordinates. (18:21) Laplace's equation (a partial differential equation), notation, overview of applications, harmonic functions, and connections to analytic functions. (27:49) Generate a harmonic function by taking the real part of an analytic function. (30:56) Find the harmonic conjugate by integration and the Cauchy-Riemann equations. (37:34) Example to illustrate a solution to Laplace's equation along the closed unit disk, using polar coordinates to describe the boundary conditions, and then imagine it to be a temperature distribution. (49:41) Infinitesimals, complex derivatives, and the amplitwist concept (due to Tristan Needham).
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
 0:57:43
0:57:43
 0:57:58
0:57:58
 0:59:16
0:59:16
 0:09:47
0:09:47
 0:51:44
0:51:44
 0:58:57
0:58:57
 0:56:18
0:56:18
 0:57:31
0:57:31
 0:12:34
0:12:34
 0:56:27
0:56:27
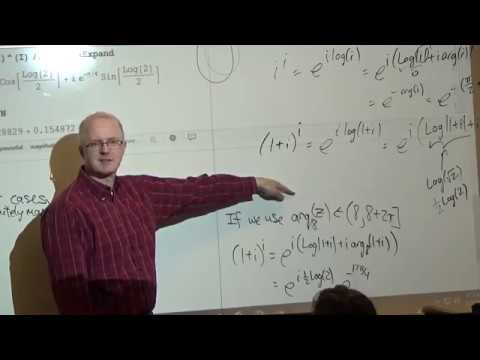 0:55:34
0:55:34
 0:55:30
0:55:30
 0:54:39
0:54:39
 0:54:09
0:54:09
 0:54:06
0:54:06
 0:58:17
0:58:17
 0:57:44
0:57:44
 0:13:15
0:13:15
 0:40:59
0:40:59
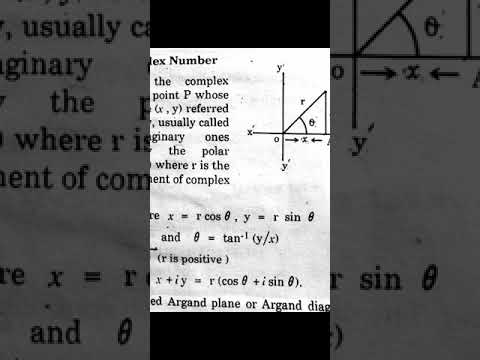 0:15:09
0:15:09
 0:53:35
0:53:35
 0:26:40
0:26:40
 0:55:15
0:55:15
 0:47:37
0:47:37