filmov
tv
Visual Group Theory, Lecture 7.1: Basic ring theory
Показать описание
Visual Group Theory, Lecture 7.1: Basic ring theory
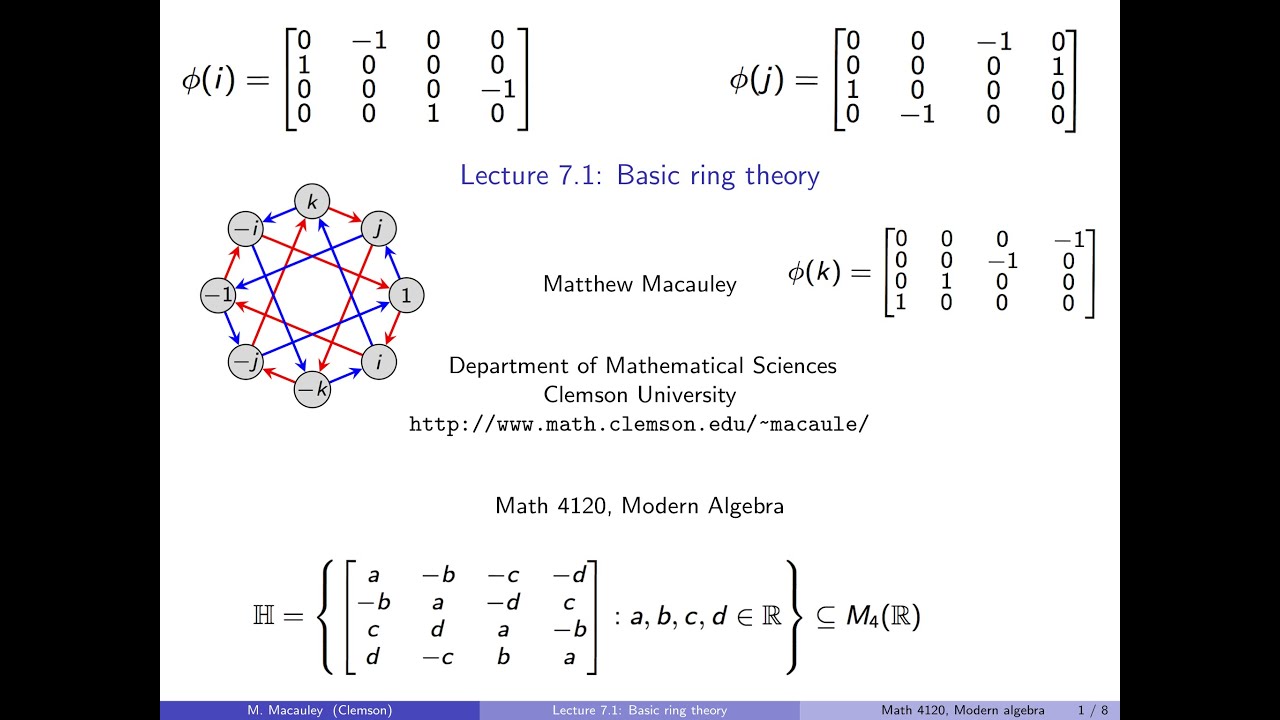
A ring is an abelian group (R,+) with a second binary operation, multiplication and the distributive law. Multiplication need not commute, nor need there be multiplicative inverses, so a ring is like a field but without these properties. Rings attempt to generalize familiar algebraic structure like the integers, reals, or complex numbers. However, many unusual things can arise: the product of nonzero elements can be zero, and ax=ay need not imply that x=y. However, these unusal properties don't happen in "integral domains", which are essentially fields without multiplicative inverses. We see a number of examples of rings, including Z, Q, R, C, Z_n, matrix rings, the Hamiltonians, and group rings.
A ring is an abelian group (R,+) with a second binary operation, multiplication and the distributive law. Multiplication need not commute, nor need there be multiplicative inverses, so a ring is like a field but without these properties. Rings attempt to generalize familiar algebraic structure like the integers, reals, or complex numbers. However, many unusual things can arise: the product of nonzero elements can be zero, and ax=ay need not imply that x=y. However, these unusal properties don't happen in "integral domains", which are essentially fields without multiplicative inverses. We see a number of examples of rings, including Z, Q, R, C, Z_n, matrix rings, the Hamiltonians, and group rings.
0:32:36
Visual Group Theory, Lecture 7.1: Basic ring theory
0:26:34
Visual Group Theory, Lecture 6.1: Fields and their extensions
0:36:34
Visual Group Theory, Lecture 5.7: Finite simple groups
0:30:09
Visual Group Theory: Lecture 7.5: Euclidean domains and algebraic integers
0:32:35
Visual Group Theory, Lecture 5.1: Groups acting on sets
0:34:20
Visual Group Theory, Lecture 7.2: Ideals, quotient rings, and finite fields
0:30:45
Visual Group Theory, Lecture 2.1: Cyclic and abelian groups
0:10:52
Lesson 7B 1 Group Multiplication Table
0:30:36
Visual Group Theory, Lecture 1.3: Groups in science, art, and mathematics
0:21:41
Group theory 7: Semidirect products
0:48:37
Visual Group Theory, Lecture 5.6: The Sylow theorems
0:21:58
Group theory, abstraction, and the 196,883-dimensional monster
0:05:30
Symmetric Groups (Abstract Algebra)
0:26:28
Visual Group Theory, Lecture 6.5: Galois group actions and normal field extensions
0:14:06
Group theory 8: Extensions
0:14:00
Visual Group Theory, Lecture 3.3: Normal subgroups
0:14:24
Group Theory 7, Subgroups
0:24:34
Visual Group Theory, Lecture 4.6: Automorphisms
0:22:46
Visual Group Theory, Lecture 3.6: Normalizers
0:07:07
Abstract Algebra 7.5: Orbits and Stabilizers
0:34:13
Visual Group Theory, Lecture 6.4: Galois groups
0:05:45
What does a ≡ b (mod n) mean? Basic Modular Arithmetic, Congruence
0:31:29
Visual Group Theory, Lecture 6.6: The fundamental theorem of Galois theory
0:35:41
Visual Group Theory, Lecture 6.2: Field automorphisms
Комментарии