filmov
tv
Intro Real Analysis, Lec 16, Part 1: Mean Value Theorem: Statement, Basic Examples, and Proof
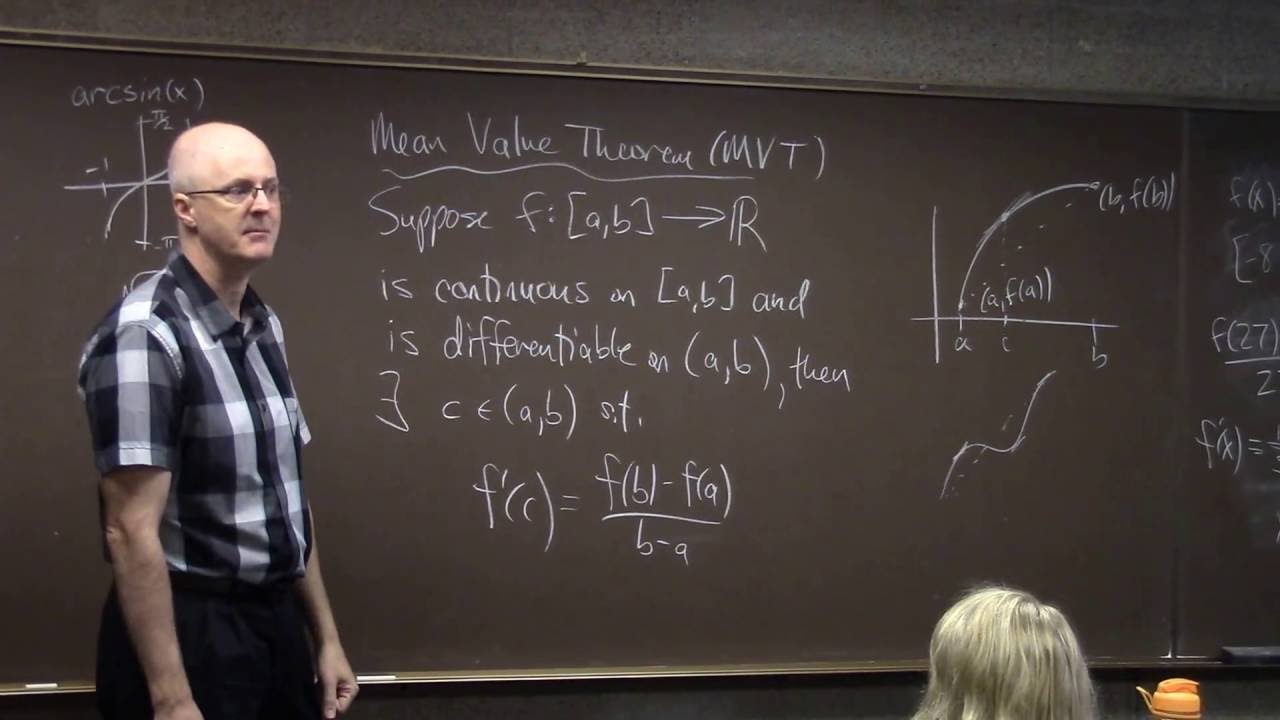
Показать описание
Introductory Real Analysis, Lecture 16, Part 1.
(0:00) Upcoming schedule.
(1:32) Statement of the Mean Value Theorem, visual interpretation, basic examples to consider.
(12:04) Deconstruction of the proof, starting with the use of Rolle's Theorem.
(20:44) Quickly run through the proof again.
(22:24) Sketch the proof of Rolle's Theorem.
(28:53) Sketch the proof of Fermat's Theorem.
Bill Kinney, Bethel University Department of Mathematics and Computer Science. St. Paul, MN.
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Intro Real Analysis, Lec 16, Part 1: Mean Value Theorem: Statement, Basic Examples, and Proof
Intro Real Analysis, Lec 16, Part 2: Summary of Corollaries of the Mean Value Theorem
Irrationals are uncountable - Lec 16 - Real Analysis
RA1.1. Real Analysis: Introduction
Intro Real Analysis, Lec 17: Mean Value Theorem Corollaries, Definition of Riemann Integral
Introduction to real analysis bartle solutions -Lec #20 Exercise#2.2 (16 to 19) #bartle
Intro Real Analysis, Lec 15: Uniform Continuity, Monotone Functions, Devil's Staircase, Derivat...
Intro Complex Analysis, Lec 16, Taylor Polynomials, Complex Exponential, Trig & Hyperbolic Funct...
Real Analysis | Infinite Series |CSIR NET 24 | IIT JAM 25 | GATE 25| Lec- 16 | VedPrep Maths Academy
Intro Real Analysis, Lec 8: Subsequences, Bolzano-Weierstrass, Cauchy Criterion, Limsup & Liminf
Lec 16: Requirement Analysis II (A)
Intro Real Analysis, Lec 9: Recursive Sequences, Limit Superior & Inferior Definitions & Pro...
Math372 Fall2017 Lec16 ConformalMaps
Intro Real Analysis, Lec 19, Part 1: Conditions for Riemann Integrability
Intro Real Analysis, Lec 5: Archimedean Property of R, Cantor's Theorem, Sequences, Crazy Funct...
Intro Real Analysis, Lec 21: Convergence of Riemann Sums, Fundamental Theorem of Calculus
Intro Real Analysis, Lec 18: Optimization Exs, Step Functions are Riemann Integrable
Lec 09: Functions and Introduction Matrix
Introductory Statistics, Lec 16A, Statistical Hypothesis Testing (for a Mean), P-value Calculations
Lec-16: Introduction to Strings🎶 in Python 🐍 with Examples | Python for Beginners
Intro Real Analysis, Lec 11: Continuity and the Intermediate Value Theorem (climbing Monk Story)
Mod-01 Lec-16
Intro Complex Analysis, Lec 5, Squaring Mapping, Euler's Identity & Trigonometry, 5th Roots...
lec 16
Комментарии
 0:33:53
0:33:53
 0:20:54
0:20:54
 0:01:22
0:01:22
 0:10:41
0:10:41
 0:56:27
0:56:27
 0:44:44
0:44:44
 0:54:44
0:54:44
 0:51:44
0:51:44
 1:51:24
1:51:24
 0:57:23
0:57:23
 0:44:58
0:44:58
 0:56:53
0:56:53
 0:50:51
0:50:51
 0:23:59
0:23:59
 0:55:02
0:55:02
 0:56:16
0:56:16
 0:56:52
0:56:52
 0:56:21
0:56:21
 0:32:46
0:32:46
 0:04:47
0:04:47
 0:56:28
0:56:28
 0:57:42
0:57:42
 0:57:44
0:57:44
 0:31:12
0:31:12