RA1.1. Real Analysis: Introduction

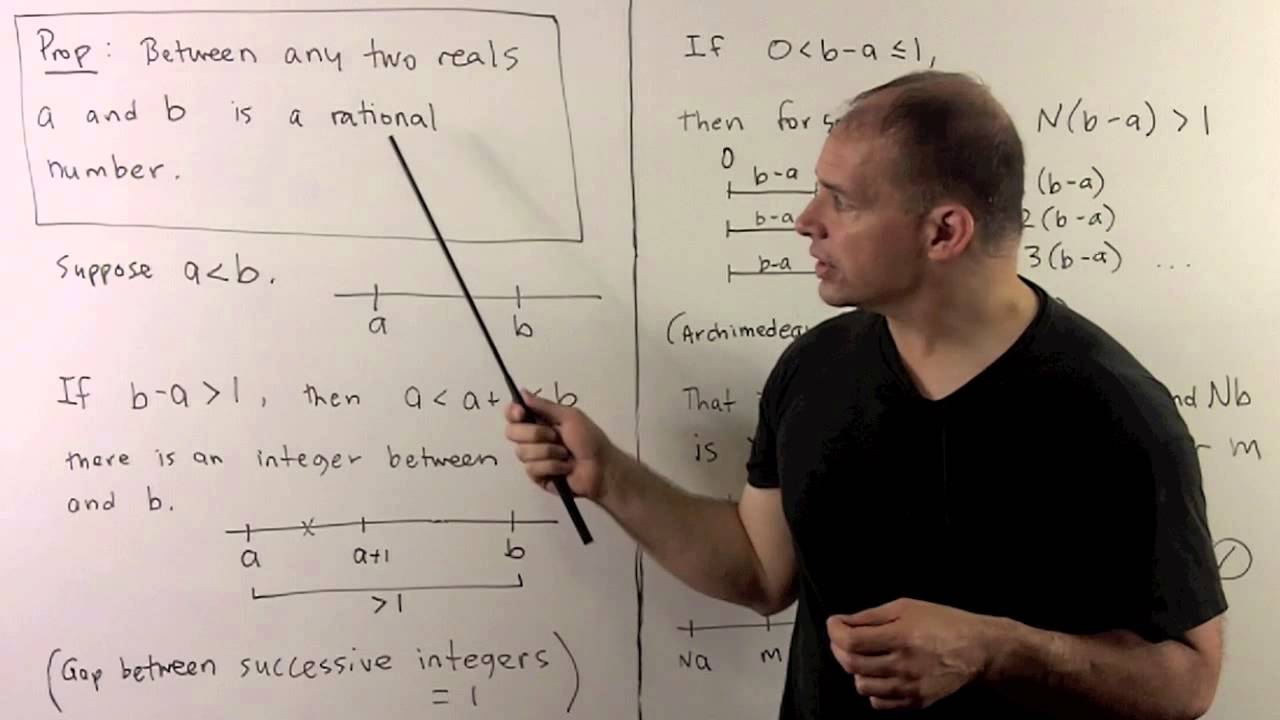
Real Analysis: We introduce some notions important to real analysis, in particular, the relationship between the rational and real numbers. Prerequisites may be found in the Math Major Basics playlist.

[MathDoctorBob]

Real Analysis and Abstract Algebra are the courses where math transitions from recipes and calculations to proofs and abstraction. Either one of these courses should start with at least a few weeks of proofs and set theory. I would never assume students know proofs for these courses beforehand.

[christocr]

That's the most straightforward and practical proof I have seen for the rational between two reals proof. Of the four analysis books I have (and several other texts that show this proof), almost all make it into brain surgery or a Rube Goldberg machine. I'll remember yours forever now because it is actually clever, direct, and elegant.

[TheReligiousAtheists]

"The rationals are like dust. They're everywhere but they weigh nothing."

*That* made it click.

[michaelraum]

These are such high quality videos, it's almost the same feeling that I have when I discover a great musician I never knew about - Bravo sir!

[magebomba]

I have watched a ton of your videos over several classes.  Clear and concise stuff, really appreciate guys and gals like yourself that take the time to upload this sort of stuff! Thanks a bunch! Hope to see you back soon!

[MariaaTKD]

You don't understand how grateful I am for these videos.Thank you so much!!

[paulchairez]

I got an A in linear algebra b/c of the doctor's videos. Now I'm studying real analysis.

[muffinspuffinsEE]

"Math isn't hard, just poorly explained" - no one ever, well except after this video

[racheljohua]

Wow seriously i atlast understand real analysis😂😂😂great video

[pauluk]

I liked this. I agree that rational numbers are sufficient to compute real world quantities with.

The 'zero measure' argument closely resembles an epsilon delta one for pointwise continuity. For every epsilon we choose we get a sum (in rational number terms) strictly less than this epsilon which 'contains' all rational numbers.

[MathDoctorBob]

Good luck on your exam! It took me a long time to warm up to analysis, but I get it now.

[MathDoctorBob]

Your welcome! We'll see how far I get this summer. I plan on covering both topics, but uniform convergence is probably far in the future.

[FPrimeHD]

Great video! My professor goes so fast it's hard to take notes keeping up with him and actually digest what he is saying.

[MathDoctorBob]

Really we need axioms before we can prove anything. Once we have the completeness axiom, we have options.

[tyroneslothdrop]

At 9:00, is what you described essentially a Cantor Set?

[robin]

On friday I have an exam on real analysis. I really love the subject.

[MathDoctorBob]

Thanks! As noted, using all the rationals is overkill - there's probably a given decimal length that will cover anything an engineer needs. We can go in the other direction also - there are no infinities in the real world, just really large natural numbers. My favorite book for this is Rudy Rucker's Infinity and the Mind.

The epsilons will be coming in full force soon enough.

[theroryfenton]

please make more videos for real analysis, PLEASE:)))

[filifur]

Very excited about R.A....hope you get to give an intro to Measure Theory....

[satyammishra]

Hi MathDoctorBob. You surely deserve more likes for the stuff you make. I am a high school student and trying to surf through the vast ocean of pure math and videos like this, on difficult topics make my journey much smoother . Keep up the good work :)