filmov
tv
Intro Real Analysis, Lec 9: Recursive Sequences, Limit Superior & Inferior Definitions & Properties
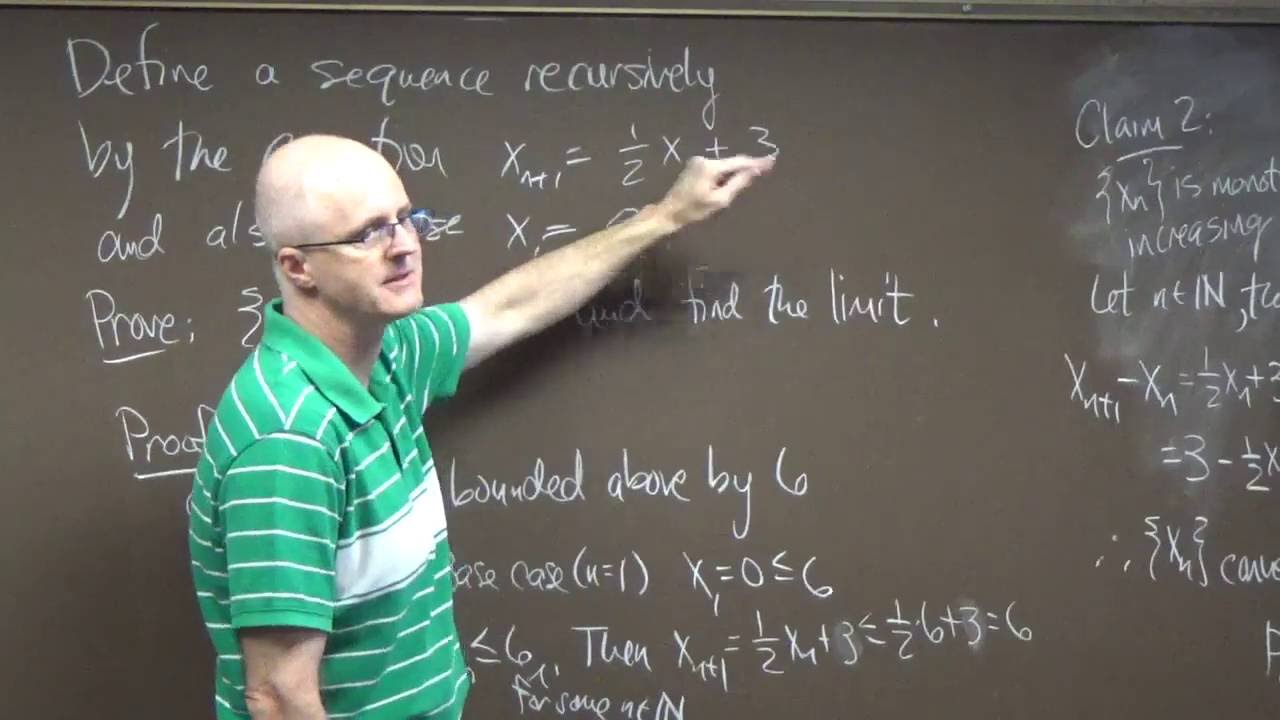
Показать описание
(0:00) Exam 1 this week and this lecture will include review.
(3:05) Recursive sequence example (prove it converges and find the limit).
(8:02) Prove the sequence example is bounded above by 6 by mathematical induction.
(10:25) Prove the sequence example is monotone increasing by using the recursive formula and the fact that the sequence is bounded above by 6 (without using induction).
(13:45) This convergent sequence does in fact converge to 6 by using algebraic properties of limits. Be careful: the sequence must be known to converge before you can algebraically solve for the limit (make cobweb plots as well).
(19:51) Definition of the limit superior (limsup) of a sequence and a visual example.
(26:10) Example 1: Relate to the theorem about how, for a bounded sequence, the limit superior is the supremum of the set of all possible subsequential limits of the sequence.
(28:36) Example 2 for this theorem.
(30:16) Example 3 for this theorem.
(31:03) Example 4 for this theorem.
(33:27) Example 5 for this theorem.
(36:54) Some properties of limit superiors and limit inferiors.
(40:05) Review: subsequence and the Bolzano-Weierstrass Theorem.
(42:58) Should understand the proof of Bolzano-Weierstrass, but it will not be on the exam.
(43:41) If a sequence has two subsequences that converge to two different numbers, than the original sequence cannot converge.
(44:15) Monotone convergence theorem (be able to prove), Cauchy sequences, and the Cauchy converge criterion.
(46:12) Definition of convergence. Convergent sequences are bounded. Squeeze theorem. Algebraic properties of limits of sequences.
(49:32) Definition of bounded, monotone, eventually monotone.
(49:58) Back to Chapter 1: increasing/decreasing function, relative maximum/minimum, cardinality of a set, a countable union of countable sets is a countable set, Q is countably infinite, R is uncountable, Completeness axiom, Archimedean property, rationals and irrationals are both dense in the reals, triangle inequality, geometric sums, ordered fields.
Bill Kinney, Bethel University Department of Mathematics and Computer Science. St. Paul, MN.
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Комментарии
 0:56:53
0:56:53
 0:10:41
0:10:41
 0:55:40
0:55:40
 0:10:34
0:10:34
 0:57:31
0:57:31
 0:21:54
0:21:54
 0:55:02
0:55:02
 0:57:23
0:57:23
 0:56:27
0:56:27
 0:57:32
0:57:32
 0:54:54
0:54:54
 0:57:48
0:57:48
 0:56:35
0:56:35
 0:20:54
0:20:54
 0:58:03
0:58:03
 0:09:53
0:09:53
 0:06:07
0:06:07
 0:56:16
0:56:16
 1:42:41
1:42:41
 0:15:07
0:15:07
 0:29:24
0:29:24
 0:11:30
0:11:30
 0:09:47
0:09:47
 0:07:51
0:07:51