filmov
tv
A Quick Functional Equation | India IMO TST 2010

Показать описание
A Super Quick and Easy Functional Equation
A Nice and Easy Functional Equation
A Quick and Easy Functional Equation from Slovenia
Solving a Quick and Easy Homemade Functional Equation
Solving a Quick and Easy Functional Equation
A Quick and Easy Functional Equation
Solving A Quick Functional Equation in Two Ways
A Functional Equation | Can you find g(x)?
Functional Equations with short Tricks Most Important topic for Exams UKPSC lecturer/UPPGT/TGT maths
A Quick and Easy Functional Equation
Solving a Quick and Easy Functional Equation
A Homemade Functional Equation | Bonus at the End
A Functional Equation with Two Functions
How To Solve A Functional Equation | The Easy Way
Solving A Quick and Fun Functional Equation
A Nice Homemade Functional Equation
A Functional Equation | Can you solve?
A Nice Functional Equation
Solving A Functional Equation
Slope of a Line | Math Hack | SAT & ACT Prep #shorts #maths
Solving a Quick and Easy Functional Equation
Solving A Functional Equation | Quick and Simple
A Short Functional Equation Problem
How REAL Men Integrate Functions
Комментарии
 0:06:49
0:06:49
 0:05:07
0:05:07
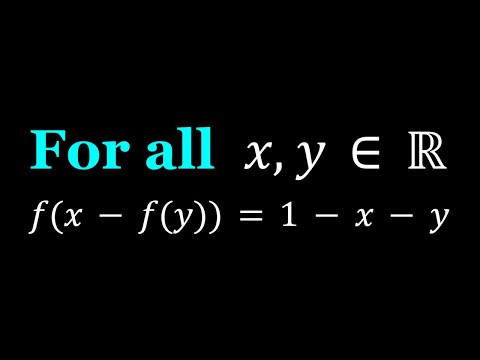 0:06:25
0:06:25
 0:05:21
0:05:21
 0:08:18
0:08:18
 0:00:57
0:00:57
 0:05:43
0:05:43
 0:04:22
0:04:22
 0:30:46
0:30:46
 0:00:45
0:00:45
 0:06:19
0:06:19
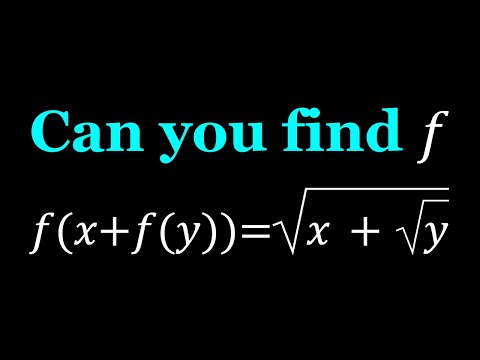 0:08:33
0:08:33
 0:06:56
0:06:56
 0:07:19
0:07:19
 0:03:56
0:03:56
 0:09:22
0:09:22
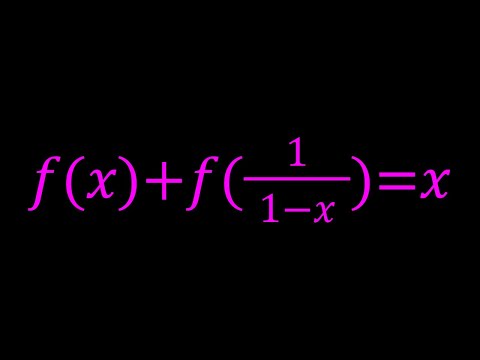 0:11:34
0:11:34
 0:08:45
0:08:45
 0:00:29
0:00:29
 0:00:17
0:00:17
 0:05:47
0:05:47
 0:05:03
0:05:03
 0:04:55
0:04:55
 0:00:35
0:00:35