filmov
tv
A Functional Equation | Can you solve?

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
f(x)+f(1/(1-x))=x
#FunctionalEquations #Functions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
f(x)+f(1/(1-x))=x
#FunctionalEquations #Functions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
A Functional Equation | Can you solve?
A Functional Equation | Can you find g(x)?
A Functional Equation from Samara Math Olympiads
How To Solve A Functional Equation | The Easy Way
Huh? How do you solve this? Functional equation for precalculus students
an absolutely surprising final solution to this functional equation.
One of the coolest functional equations I have seen!
A Cool Functional Equation
South Korea ! Can you find 'X' - Calling all Algebra Lovers! #maths #algebra #findx #olymp...
A Nice Functional Equation #maths #matholympiad #education #functions #function
a functional equation
Solving A Functional Equation
a FUNctional equation...
A functional equation from Kyrgyzstan
A Nice and Easy Functional Equation
Solving A Nice Functional Equation
A functional equation from my favorite book.
Solving a functional equation in 45 seconds #maths #shorts
A Curious Functional Equation | Math Olympiads
Solving a Quick and Easy Functional Equation
the greatest functional equation of all time.
a notorious functional equation.
an IMO functional equation.
Methods of Functional Equations
Комментарии
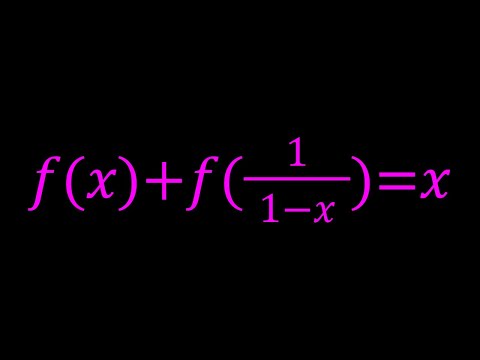 0:11:34
0:11:34
 0:04:22
0:04:22
 0:08:47
0:08:47
 0:07:19
0:07:19
 0:05:46
0:05:46
 0:18:15
0:18:15
 0:15:34
0:15:34
 0:05:38
0:05:38
 0:20:13
0:20:13
 0:00:44
0:00:44
 0:16:24
0:16:24
 0:00:29
0:00:29
 0:16:40
0:16:40
 0:12:02
0:12:02
 0:05:07
0:05:07
 0:09:50
0:09:50
 0:11:23
0:11:23
 0:00:46
0:00:46
 0:08:29
0:08:29
 0:08:18
0:08:18
 0:07:48
0:07:48
 0:19:30
0:19:30
 0:14:31
0:14:31
 0:07:40
0:07:40