filmov
tv
A Quick and Easy Functional Equation from Slovenia

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
A Quick and Easy Functional Equation
Solving a Quick and Easy Functional Equation
Solving a Quick and Easy Functional Equation
Solving a Quick and Easy Functional Equation
A Quick and Easy Functional Equation from Slovenia
Solving a Quick and Easy Homemade Functional Equation
A Nice and Easy Functional Equation
Learn Functional Groups FAST (Organic Chemistry)
An Easy Home Functional Training Workout for Beginners (Can't Do a Push up? No Problem!)
Creating A Functional And Perfect Bedroom In A Two-Square-Meter Space #shorts
#maths | A Quick And Easy Functional Equation | #function #youtubevideos
Agility Ladder Drills (Cardio + Functional)
Multi - Functional Woodworking Machine by SN Tools Sliding Table Saw Cutting Machine - 1386#shorts
Functional Requirements and Specifications: A Quick Tutorial
TOP 10 IKEA HACKS | easy, functional & aesthetic (full tutorials)
Functional Harmony - Music Theory Lesson
Functional Training
Functional programming - A general introduction
Cost affordable, easy to build, and functional! We love our DIY paver patio #beforeafter #diypatio
Results Plus for Functional Skills: A quick guide...
Functional Groups
Functional Groups with Memorization Tips
Making a Fully Functional Jet Engine using Soda can | diy Jet Engine
Functional Training Circuit | Mirafit
Комментарии
 0:06:49
0:06:49
 0:08:18
0:08:18
 0:06:19
0:06:19
 0:05:47
0:05:47
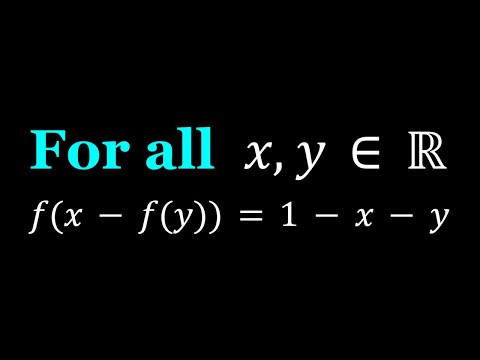 0:06:25
0:06:25
 0:05:21
0:05:21
 0:05:07
0:05:07
 0:03:51
0:03:51
 0:17:35
0:17:35
 0:00:54
0:00:54
 0:08:09
0:08:09
 0:00:16
0:00:16
 0:00:30
0:00:30
 0:15:03
0:15:03
 0:28:46
0:28:46
 0:07:59
0:07:59
 0:00:46
0:00:46
 0:11:47
0:11:47
 0:00:13
0:00:13
 0:05:02
0:05:02
 0:04:43
0:04:43
 0:21:19
0:21:19
 0:16:27
0:16:27
 0:00:26
0:00:26