filmov
tv
Solving Nice Exponential Equation | Solve x=x^2+6x^1/2. | Exponential Equation | Algebra.
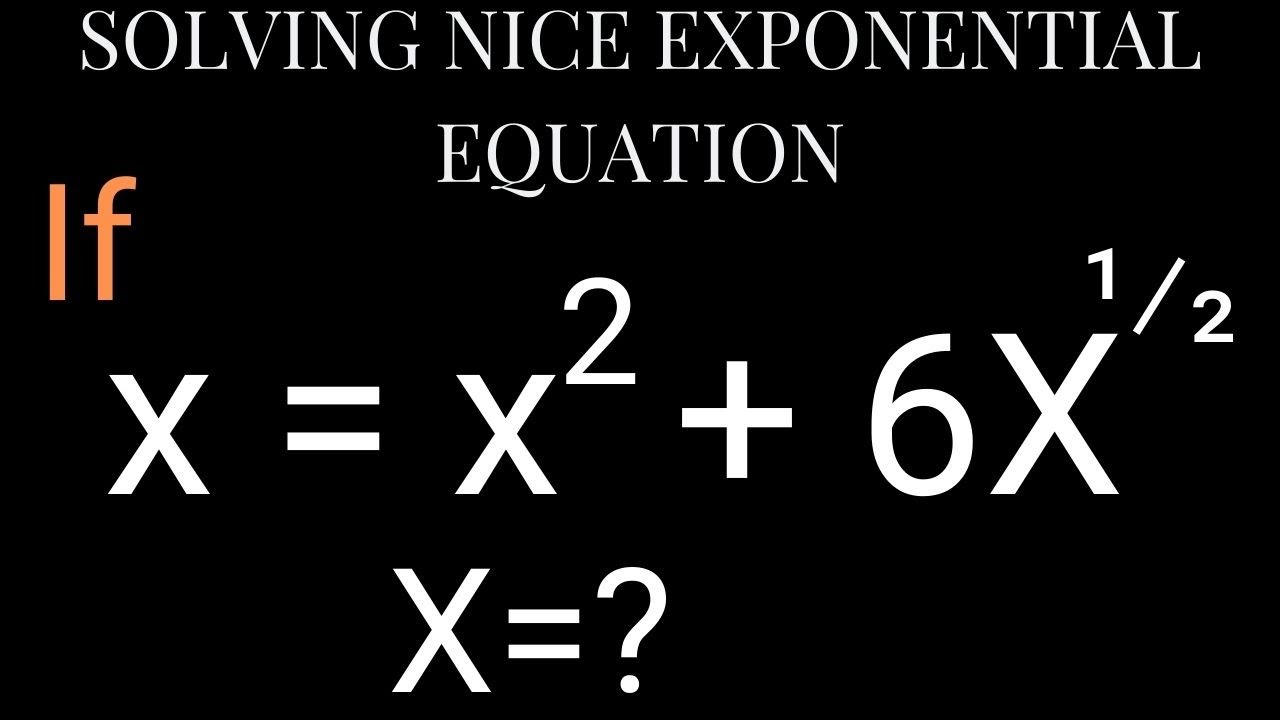
Показать описание
Solving Nice Exponential Equation x=x^2+6x^1/2. Solving Exponential or radical Equation Systematically is one of the best video on algebraic simplification you will ever enjoy watching as it is loaded with so many insights and tricks into solving exponential equations of this kind. #algebra #exponentialequations #olympiadmathematics #factorization #simplification
In this video, you will learn how to introduce another alphabet to replace the square root from the expression and simplify systematically according to the algebraic terms and signs involve.
You will learn how to form a quartic equation from the radical equation above and how to factorize the quartic equation completing. Here, you will learn how to use the trial by error method to solve polynomial equations also.
You will also learn how to create a quartic equation from the above exponential equation the easy way. I will show you how to solve the resulted quadratic equation by using the factorization method in order to get x variable.
Above all, if you are new to this channel please kindly subscribe and turn on the bell notification button in order to get all newly uploaded videos as we upload at least a video everyday in this channel.
Thanks for being there.
#exponentialequations #olympiadmathematics #polynomials #polynomialsandfactorisation9thclassapandts #olympiadmathematicscompetition #olympiad #exponents #exponential #mathematics #solvingproblems #solving #matholympiadquestion #matholympiadpreparation #matholympiadtraining #blackpenredpen #matholympiad #olympiad2022 #equation #equations #algebra #algebratricks #algebraicexpression #algebraic #algebraicequation #solution #solutions #mathchallenge #tricks #factorization #factors #simplification #quadraticequation #quadraticequations #quadratic #quadratic #formula #algebra #mathstrick #exponents #mathsskills #exponential #algebra #solutions
In this video, you will learn how to introduce another alphabet to replace the square root from the expression and simplify systematically according to the algebraic terms and signs involve.
You will learn how to form a quartic equation from the radical equation above and how to factorize the quartic equation completing. Here, you will learn how to use the trial by error method to solve polynomial equations also.
You will also learn how to create a quartic equation from the above exponential equation the easy way. I will show you how to solve the resulted quadratic equation by using the factorization method in order to get x variable.
Above all, if you are new to this channel please kindly subscribe and turn on the bell notification button in order to get all newly uploaded videos as we upload at least a video everyday in this channel.
Thanks for being there.
#exponentialequations #olympiadmathematics #polynomials #polynomialsandfactorisation9thclassapandts #olympiadmathematicscompetition #olympiad #exponents #exponential #mathematics #solvingproblems #solving #matholympiadquestion #matholympiadpreparation #matholympiadtraining #blackpenredpen #matholympiad #olympiad2022 #equation #equations #algebra #algebratricks #algebraicexpression #algebraic #algebraicequation #solution #solutions #mathchallenge #tricks #factorization #factors #simplification #quadraticequation #quadraticequations #quadratic #quadratic #formula #algebra #mathstrick #exponents #mathsskills #exponential #algebra #solutions
Комментарии
 0:02:34
0:02:34
 0:04:25
0:04:25
 0:09:19
0:09:19
 0:16:36
0:16:36
 0:10:28
0:10:28
 0:08:50
0:08:50
 0:09:56
0:09:56
 0:06:37
0:06:37
 0:09:21
0:09:21
 0:05:34
0:05:34
 0:06:50
0:06:50
 0:08:21
0:08:21
 0:11:14
0:11:14
 0:10:34
0:10:34
 0:00:55
0:00:55
 0:03:03
0:03:03
 0:09:59
0:09:59
 0:00:56
0:00:56
 0:00:31
0:00:31
 0:10:27
0:10:27
 0:10:02
0:10:02
 0:02:01
0:02:01
 0:08:36
0:08:36
 0:08:26
0:08:26