filmov
tv
Lebesgue Integral Example

Показать описание
As promised, in this video I calculate an explicit example of a Lebesgue integral. As you'll see, it's a much more efficient way of calculating the area under that curve. Finally, I'll present a really cool way of doing this problem. Enjoy!
A horizontal integral?! Introduction to Lebesgue Integration
Lebesgue Integral Example
Lebesgue Integral Overview
Lebesgue Integral|difference b/w Lebesgue and Riemann Integral| examples of Lebesgue integral LEC 13
Lebesgue Integration 2: Lebesgue Integral of Simple Functions
SIT3001 Week 6 (The Lebesgue integral)
Lebesgue Integration|Examples of Lebesgue integrable functions
Measure Theory, Functional Analysis, and The Lebesgue Integral for Undergraduates - Johnston
3 Integrals You Won't See in Calculus (And the 2 You Will)
Lebesgue integral[ Definition and Example], Lebesgue measure and integral, lecture-11
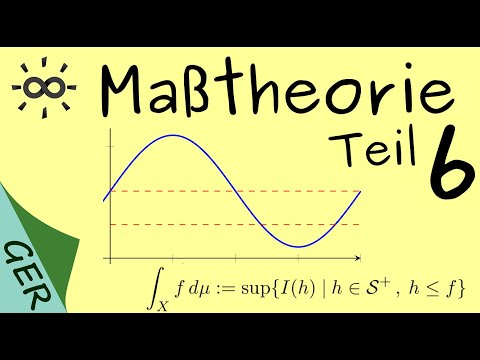
Maßtheorie - Teil 6 - Lebesgue-Integral
Riemann integral vs. Lebesgue integral [dark version]
3 key differences between Riemann and Lebesgue integrals!
Lebesgue Integration -- simple problems
Construction of the Lebesgue Integral
Lecture 12: Lebesgue Integrable Functions, the Lebesgue Integral and the Dominated Convergence...
Lebesgue Integral of a nonnegative function part I
Lebesgue Integral Animation
Riemann-Integral vs. Lebesgue-Integral
Measure Theory 6 | Lebesgue Integral [dark version]
Measure and Integration 17 - General Lebesgue Integral
Riemann vs Lebesgue Integral
Stochastik 1: VL9 -- Lebesgue-Integration
Lebesgue Integral Exercises
Комментарии
 0:09:54
0:09:54
 0:22:52
0:22:52
 0:26:23
0:26:23
 0:14:39
0:14:39
 0:19:01
0:19:01
 1:33:35
1:33:35
 0:35:38
0:35:38
 0:15:46
0:15:46
 0:12:05
0:12:05
 0:21:36
0:21:36
 0:23:49
0:23:49
 0:19:39
0:19:39
 0:02:15
0:02:15
 0:08:13
0:08:13
 0:16:42
0:16:42
 1:24:57
1:24:57
 0:40:03
0:40:03
 0:00:35
0:00:35
 0:14:49
0:14:49
 0:23:16
0:23:16
 0:49:50
0:49:50
 0:13:52
0:13:52
 1:40:44
1:40:44
 0:16:52
0:16:52