filmov
tv
3 Integrals You Won't See in Calculus (And the 2 You Will)

Показать описание
In Calculus, we usually learn the Riemann integral, or sometimes the Darboux integral in disguise. But there are many problems these integrals can't solve! Like if we want to integrate a function which is discontinuous everywhere, or if we want to integrate with respect to a random process. Let's explore 5 different integrals, starting with the 2 you might see in Calculus, and then 3 more advanced integrals that are often only seen in graduate school -- the Riemann-Stieltjes integral, Lebesgue integral, and Itô integral!
00:00 Introduction
00:32 Level 1 -- Riemann Integral
01:58 Level 2 -- Darboux Integral
04:00 Level 3 -- Riemann-Stieltjes
07:02 Level 4 -- Lebesgue Integral
09:57 Level 5 -- Itô Integral
00:00 Introduction
00:32 Level 1 -- Riemann Integral
01:58 Level 2 -- Darboux Integral
04:00 Level 3 -- Riemann-Stieltjes
07:02 Level 4 -- Lebesgue Integral
09:57 Level 5 -- Itô Integral
Integration Tricks (That Teachers Won't Tell You) for Integral Calculus
How to change the order of a triple integral
Calculus 3: Line Integrals (18 of 44) What is a Line Integral? [(y)dx+(z)dy+(x)dz] Example 6
How to do two (or more) integrals with just one
Learn to Solve an Integral (What Makes You Beautiful Parody) AP Calculus BC
What Integration Technique Should I Use? (trig sub, u sub, DI method, partial fractions) calculus 2
Integration in Spherical Coordinates
It 'Cannot' Be Done (Integrals)
Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus
How to evaluate the integral given different integrands
How to Set Up Double Integrals
Calculus 3: Triple Integrals (1 of 25) What is a Triple Integral?
Integration (Calculus)
What is Double integral? Triple integrals? Line & Surface integral? Volume integral? #SoME2
Integration of Rational Functions into Logarithms By Substitution & Long Division
What are double integrals? What are they for? | #SoME1 #3b1b
Integrals: degree of top GREATER than bottom. #calculus #integrals #mathchallenge #mathtricks
Integral of t*e^(-3t) with integration by parts
One weird integral trick
Triple integrals to find volume of the solid (KristaKingMath)
Every Student Should See This
Why I don't teach LIATE (integration by parts trick)
Improper Integrals - Convergence and Divergence - Calculus 2
Understand u substitution for integration (3 slightly trickier examples), calculus 1 tutorial
Комментарии
 0:11:26
0:11:26
 0:09:40
0:09:40
 0:05:03
0:05:03
 0:18:03
0:18:03
 0:03:39
0:03:39
 0:22:40
0:22:40
 0:07:52
0:07:52
 0:03:11
0:03:11
 0:20:46
0:20:46
 0:09:22
0:09:22
 0:08:56
0:08:56
 0:09:14
0:09:14
 0:07:04
0:07:04
 0:05:59
0:05:59
 0:19:20
0:19:20
 0:15:34
0:15:34
 0:00:48
0:00:48
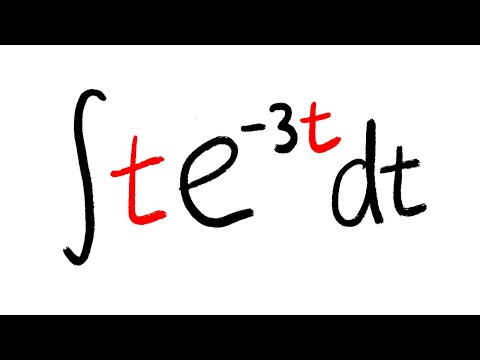 0:04:58
0:04:58
 0:01:00
0:01:00
 0:14:03
0:14:03
 0:00:58
0:00:58
 0:14:54
0:14:54
 0:13:56
0:13:56
 0:14:41
0:14:41