filmov
tv
A horizontal integral?! Introduction to Lebesgue Integration

Показать описание
More applications!
Follow me!
A horizontal integral?! Introduction to Lebesgue Integration
Horizontal and Vertical Integration (Business Growth Strategy)
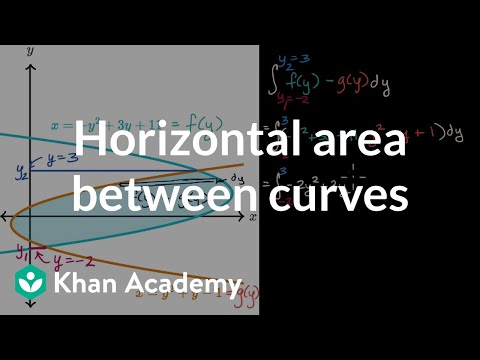
Horizontal area between curves | Applications of definite integrals | AP Calculus AB | Khan Academy
Calculus 2 - Integration: Finding the Area Between Curves (12 of 22) Horizontal dA
Double Integrals Using Vertical and Horizontal Cross-sections
Horizontal Integration
Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus
Vertical vs. Horizontal Integration
Horizontal Integration
Disk & Washer Method - Calculus
Horizontal, vertical and conglomerate integration
Properties of Integrals and Evaluating Definite Integrals
Finding the Area Between Two Curves by Integration
Integrals and Volumes: Example 5 Rotating About a Horizontal Line
Definite integrals intro | Accumulation and Riemann sums | AP Calculus AB | Khan Academy
Horizontal integration | meaning of Horizontal integration
Differences between Horizontal and Vertical Integration.
What is Jacobian? | The right way of thinking derivatives and integrals
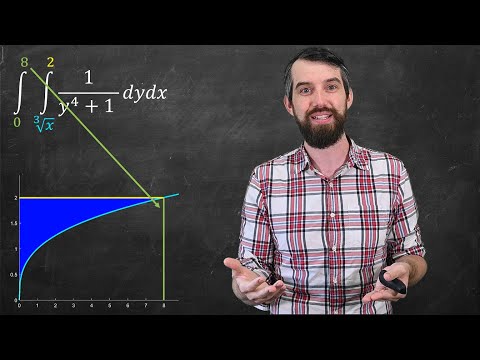
Change the order of integration to solve tricky integrals
Calculus 2 (203) -5.2 - Area using Horizontal Slices
Integration Problem - Area Between Two Curves - Using Horizontal Rectangles - Exam Question Example
Business Growth: Advantages and Drawbacks of Horizontal Integration I A Level and IB Economics
Find the vertical and horizontal asymptotes
Volumes Using Cross Sections - Calculus
Комментарии
 0:09:54
0:09:54
 0:05:22
0:05:22
 0:08:03
0:08:03
 0:05:42
0:05:42
 0:17:20
0:17:20
 0:00:40
0:00:40
 0:20:46
0:20:46
 0:02:24
0:02:24
 0:03:04
0:03:04
 0:20:00
0:20:00
 0:03:33
0:03:33
 0:09:48
0:09:48
 0:07:52
0:07:52
 0:10:14
0:10:14
 0:07:53
0:07:53
 0:00:36
0:00:36
 0:02:20
0:02:20
 0:27:14
0:27:14
 0:07:39
0:07:39
 0:11:48
0:11:48
 0:08:26
0:08:26
 0:06:51
0:06:51
 0:03:54
0:03:54
 0:11:46
0:11:46