Limit of sinx^2/x as x approaches 0 | Calculus 1 Exercises

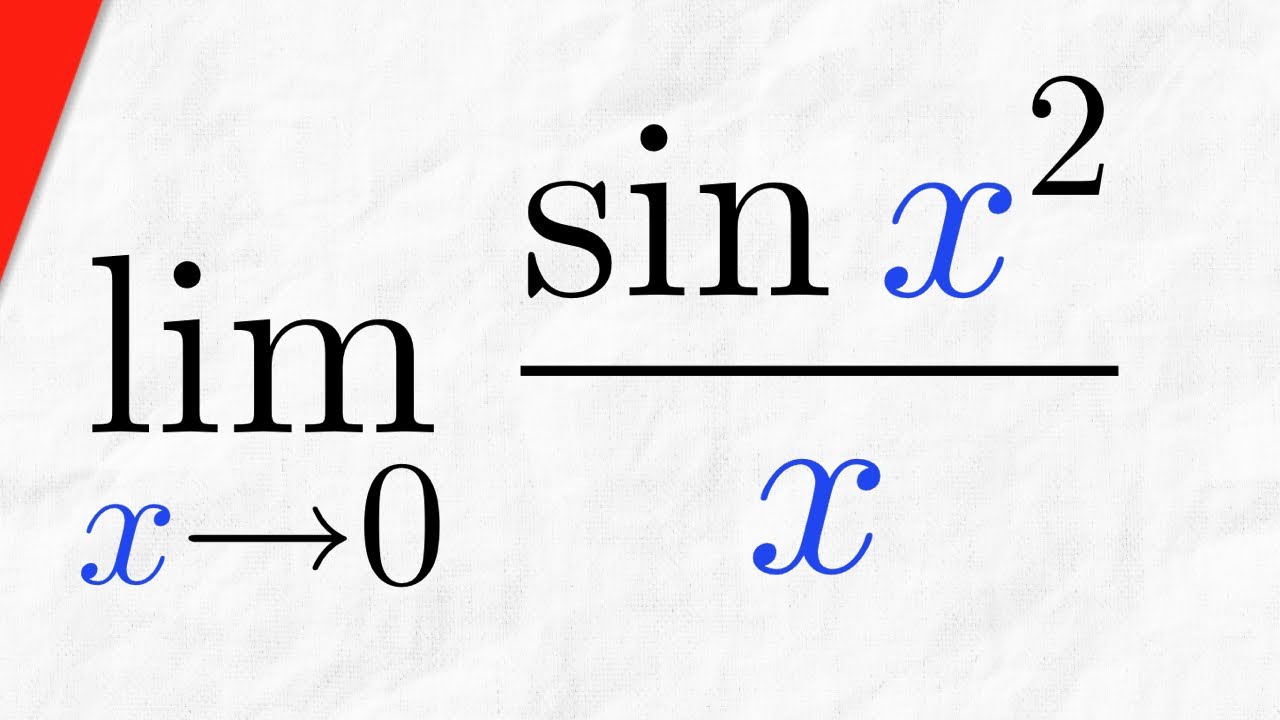
preview_player
Показать описание
We evaluate the limit of sin(x^2)/x as x approaches 0 by multiplying the limit by x/x, then apply the limit product law to separate it into two easy limits. The first is limit of sinx/x as x approaches 0, and the second is simply x. Easy! #Calculus1 #APCalculus

◉Textbooks I Like◉

★DONATE★

Thanks to Petar, dric, Rolf Waefler, Robert Rennie, Barbara Sharrock, Joshua Gray, Karl Kristiansen, Katy, Mohamad Nossier, and Shadow Master for their generous support on Patreon!

Follow Wrath of Math on...

  1. Wrath of Math
  2. wrath of math
  3. math lessons
  4. math
  5. education
  6. math video
Рекомендации по теме
Limit of sinx^2/x 0:03:02

Limit of sinx^2/x as x approaches 0 | Calculus 1 Exercises

Limit of sin(2x)/x 0:05:31

Limit of sin(2x)/x as x approaches 0 | Calculus 1 Exercises

Limit sin2x/x as 0:01:09

Limit sin2x/x as x tends to 0

Limit of sin(x)/x 0:03:59

Limit of sin(x)/x as x goes to Infinity (Squeeze Theorem) | Calculus 1 Exercises

Limit x^2(3 + 0:03:26

Limit x^2(3 + sin(x))/(x + sin(x))^2 as x approaches zero Calculus 1 Limits with sinx/x

Limits of Trigonometric 0:15:23

Limits of Trigonometric Functions

Limit of sin(x/2) 0:00:47

Limit of sin(x/2) as x Approaches pi #shorts #calculus

Limit of sin(3x)/2x 0:03:20

Limit of sin(3x)/2x as x approaches 0, (check desc. for similar videos)

L19 KCET 2025 0:59:46

L19 KCET 2025 Maths Course | Continuity & Differentiability Complete Revision & PYQs

Evaluate the limit 0:03:28

Evaluate the limit of sinx over x

How to solve 0:03:02

How to solve limit of sin(2x)/sin(5x) as x approaches 0

Proof: Limit of 0:10:21

Proof: Limit of sinx/x as x approaches 0 with Squeeze Theorem | Calculus 1

Limit of (2sin 0:03:46

Limit of (2sin x - sin 2x)/x^3 as x approaches 0

Limit of sin(x)/x 0:02:22

Limit of sin(x)/x as x approaches 0 (Proof) | Derivative rules | Science Valhalla

Limit sin(2x)/x as 0:00:41

Limit sin(2x)/x as x approaches 0, 35 seconds

Limit of sin(3x)/x 0:02:59

Limit of sin(3x)/x as x approaches 0 | Calculus 1 Exercises

Limit of (tan 0:03:22

Limit of (tan 2x - x)/(3x - sin x) as x approaches 0

Find the limit 0:02:50

Find the limit as x approaches 0 of (sin x- 2 sin 2x)/(x cos x)

lim as x 0:00:38

lim as x approaches 0, sin x / 2x

Find the limit 0:03:18

Find the limit as x approaches 0 for (e^x -e^(-x) - 2x)/(x - sin x). l’Hopital’s Rule

Limit of sin^8(x)/x 0:02:40

Limit of sin^8(x)/x as x approaches 0

lim Sinx/x as 0:00:22

lim Sinx/x as x tends to infinity ,# Easy # Short # Trick

Limit of (sinx/x)^1/x^2 0:04:24

Limit of (sinx/x)^1/x^2 as x approaches 0

Limit of x*sin(1/x) 0:08:14

Limit of x*sin(1/x) as x approaches 0 | Calculus 1 Exercises

Комментарии
Автор

Help support the production of this course by joining Wrath of Math to access exclusive and early Calc 1 videos, plus lecture notes at the premium tier!

WrathofMath
Автор

Thank you Much....I was having such a hard time with this & the Solution was a piece of Cake ❤️

xyco_edits
Автор

I learn calculus on my own and used de l' Hospital. But good to see other ways too to get more varied and more in depth what can work too.

pianoplayerable
Автор

For the x^2 I just did (x * x) and sin x/x = 1 then just did dirext substitution which is x = 0*1. Did I disobey any math rules?

doggy
Автор

You can use L’hospitals rule to as you get 0/0 in the first direct substitution. This gives (2xcosx^2)/1 which equals 0/1 =0. Though in all honesty the squeeze theorem and product rule are fun too.

mooblerthomson
Автор

Evaluate lim x -> 0 (sin x ^ 2 - sin^2 x)/(x ^ 4) Can you solve this sir

usthestarboom
Автор

Can you explain about limit x^2 approach 0 ?

サバトラ-mn
Автор

Now I wonder what sin(sqrt(x))/x goes to as x goes to zero?

alessandrorossi