filmov
tv
Limit of sin(2x)/x as x approaches 0 | Calculus 1 Exercises
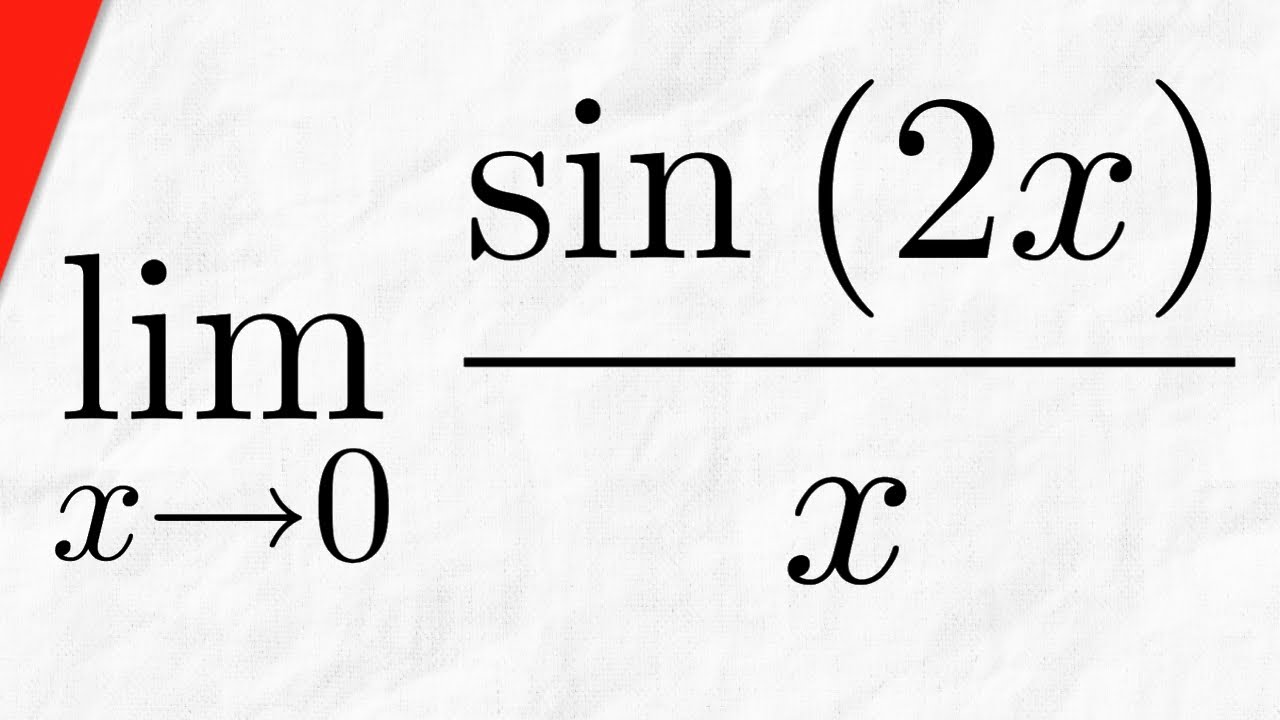
Показать описание
We show the limit of sin(2x)/x as x goes to 0 is equal to 2. To evaluate this trigonometric limit, we need to remember the limit of sin(x)/x with x approaching 0, which is a fundamental trigonometric limit equal to 1! If we remember this, we'll be able to solve the problem in short order. #Calculus1
Proof for Limit of sin(x)/x: (coming soon):
★DONATE★
Thanks to Robert Rennie, Barbara Sharrock, and Rolf Waefler for their generous support on Patreon!
Follow Wrath of Math on...
Proof for Limit of sin(x)/x: (coming soon):
★DONATE★
Thanks to Robert Rennie, Barbara Sharrock, and Rolf Waefler for their generous support on Patreon!
Follow Wrath of Math on...
0:05:31
Limit of sin(2x)/x as x approaches 0 | Calculus 1 Exercises
0:03:02
Limit of sinx^2/x as x approaches 0 | Calculus 1 Exercises
0:01:09
Limit sin2x/x as x tends to 0
0:00:44
Unveiling the Mystery of sin(2x)/x: Solving the Limit as x Approaches 0 using 2/2
0:00:41
Limit sin(2x)/x as x approaches 0, 35 seconds
0:08:14
Find the lim x approaches 0: sin2x/x
0:00:48
Calculus: Limit of sin(2x)/(3x) as x goes to 0, done in 45 seconds!
0:02:40
Limit of sin^8(x)/x as x approaches 0
0:15:23
Limits of Trigonometric Functions
0:06:15
Limit of sin(kx)/x as x approaches 0 | Calculus 1 Exercises
0:03:19
Limit of sin^2x/(x cosx) ❖ Calculus 1 ❖ Trig Limits
0:00:53
lim x->0 sin 2x/x=
0:02:59
Limit of sin(3x)/x as x approaches 0 | Calculus 1 Exercises
0:04:47
Limit of (sin 2x)/(2x^2 + x) ❖ Calculus 1
0:03:59
Limit of sin(x)/x as x goes to Infinity (Squeeze Theorem) | Calculus 1 Exercises
0:11:55
lim x approaches 0: sin2x/x, sin3x/x, sin4x/x, sin5x/x
0:03:20
Limit of sin(3x)/2x as x approaches 0, (check desc. for similar videos)
0:01:36
Find the limit lim t = 0 of sin^2(3t)/t^2
0:03:58
Limit of tan^2x/x as x approaches 0 (without L'Hospital's Rule!) | Calculus 1 Exercises
0:03:20
Learn how to evaluate the limit at infinity of a trigonometric function
0:03:26
Evaluate lim x → 0 sin2x/x || Limit(x→0) sin 2x/x
0:00:11
IIT Bombay CSE 😍 #shorts #iit #iitbombay
0:03:04
Find the limit of sin(2x)/tan(3x) as x approaches 0
0:03:02
How to solve limit of sin(2x)/sin(5x) as x approaches 0
Комментарии