Limit of sin(x)/x as x goes to Infinity (Squeeze Theorem) | Calculus 1 Exercises

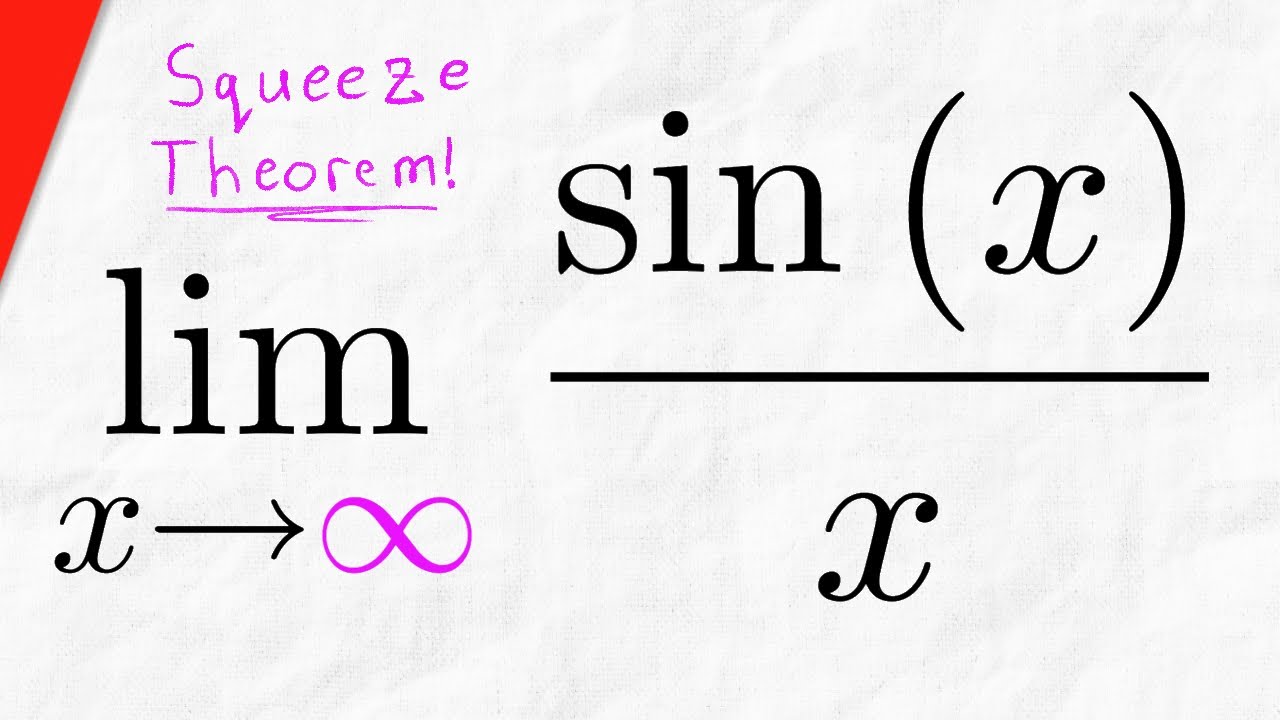
preview_player
Показать описание
We use the squeeze theorem to evaluate the limit of sinx/x as x approaches infinity. This is easy as soon as we recall -1 is less than or equal to sin(x) is less than or equal to 1, then just divide everything by x! #Calculus1

◉Textbooks I Like◉

★DONATE★

Thanks to Petar, dric, Rolf Waefler, Robert Rennie, Barbara Sharrock, Joshua Gray, Karl Kristiansen, Katy, Mohamad Nossier, and Shadow Master for their generous support on Patreon!

Follow Wrath of Math on...

  1. Wrath of Math
  2. wrath of math
  3. math lessons
  4. math
  5. education
  6. math video
Рекомендации по теме
Limit of sin(x)/x 0:09:16

Limit of sin(x)/x as x approaches 0 | Derivative rules | AP Calculus AB | Khan Academy

Proving a Limit 0:01:00

Proving a Limit of sin(x)/x

Limit of sin(x)/x 0:03:59

Limit of sin(x)/x as x goes to Infinity (Squeeze Theorem) | Calculus 1 Exercises

The most important 0:11:54

The most important limit in Calculus // Geometric Proof & Applications

Proof: Limit of 0:10:21

Proof: Limit of sinx/x as x approaches 0 with Squeeze Theorem | Calculus 1

Limit of sin(x)/x 0:02:22

Limit of sin(x)/x as x approaches 0 (Proof) | Derivative rules | Science Valhalla

The Limit (do 0:12:08

The Limit (do not use L'Hospital rule)

Limit of sin(x)/x: 0:05:27

Limit of sin(x)/x: Detailed Explanation and Proof

Calculus 1 Exam 3:10:17

Calculus 1 Exam Review Part8

Squeeze Theorem with 0:00:59

Squeeze Theorem with sin(x) #shorts

Two Trig Limits 0:00:58

Two Trig Limits YOU NEED for AP Calc Exam

Limits of Trigonometric 0:15:23

Limits of Trigonometric Functions

the most controversial 0:08:19

the most controversial limit in calculus 1

Limit of sin(kx)/x 0:06:15

Limit of sin(kx)/x as x approaches 0 | Calculus 1 Exercises

Limit of sin^8(x)/x 0:02:40

Limit of sin^8(x)/x as x approaches 0

Calculus 1: Limits 0:15:53

Calculus 1: Limits of sin(x)/x and (1 - cos(x))/x as x approaches zero

Limit of sin(x) 0:01:36

Limit of sin(x) / x as x → 0 – a geometric proof

Limit of sin(x)/sinh(x) 0:00:40

Limit of sin(x)/sinh(x) as x approaches 0 using L'Hopital's Rule #shorts

Visualizing the derivative 0:00:59

Visualizing the derivative of sin(x)

Limit of sin(ax)/x 0:03:46

Limit of sin(ax)/x as x approaches 0 (No L'Hopital's Rule!)

Calculus - How 0:11:01

Calculus - How to find trigonometric limits using sin(x)/x

Limit of sin(7x)/sin(3x) 0:01:46

Limit of sin(7x)/sin(3x) as x Approaches Zero

How to Find 0:00:40

How to Find the Limit of sin(x + sin(x)) as x approaches Pi #shorts

This is a 0:00:48

This is a very famous limit

Комментарии
Автор

Help me produce this course by joining Wrath of Math to access exclusive and early Calc 1 videos, plus lecture notes at the premium tier!

WrathofMath
Автор

appreciate this! very well explained :))

princessatellaluma
Автор

How would you do the epsilon-delta on this? I can't come up with a way to prove the limit of sinx / x, but I can prove the limit of x / sinx pretty simply. Is it acceptable to do epsilon-delta on the reciprocal of a function, and then invoke the reciprocal rule of limits?

kingbeauregard
Автор

You have managed to squeeze a very important lesson from this example! 😃

punditgi
Автор

Lim 1/1+n sin^2(pi x), x tends to zero, please do it and send me

safiurmallick
Автор

How can we fine Lim x approaches infinity x+sinx/x

GhazanfarAli-ofyt
Автор

What if limit x--->0 ??.? For the same question

AmitaKumari-yqbd
Автор

Is this following sendwitch theorem ... ?

about_nasa_videos
Автор

You need to work on your calculus as the limit is 1 and not 0. Look at the graph you showed.

elviszavatti