Proof: Limit of sinx/x as x approaches 0 with Squeeze Theorem | Calculus 1

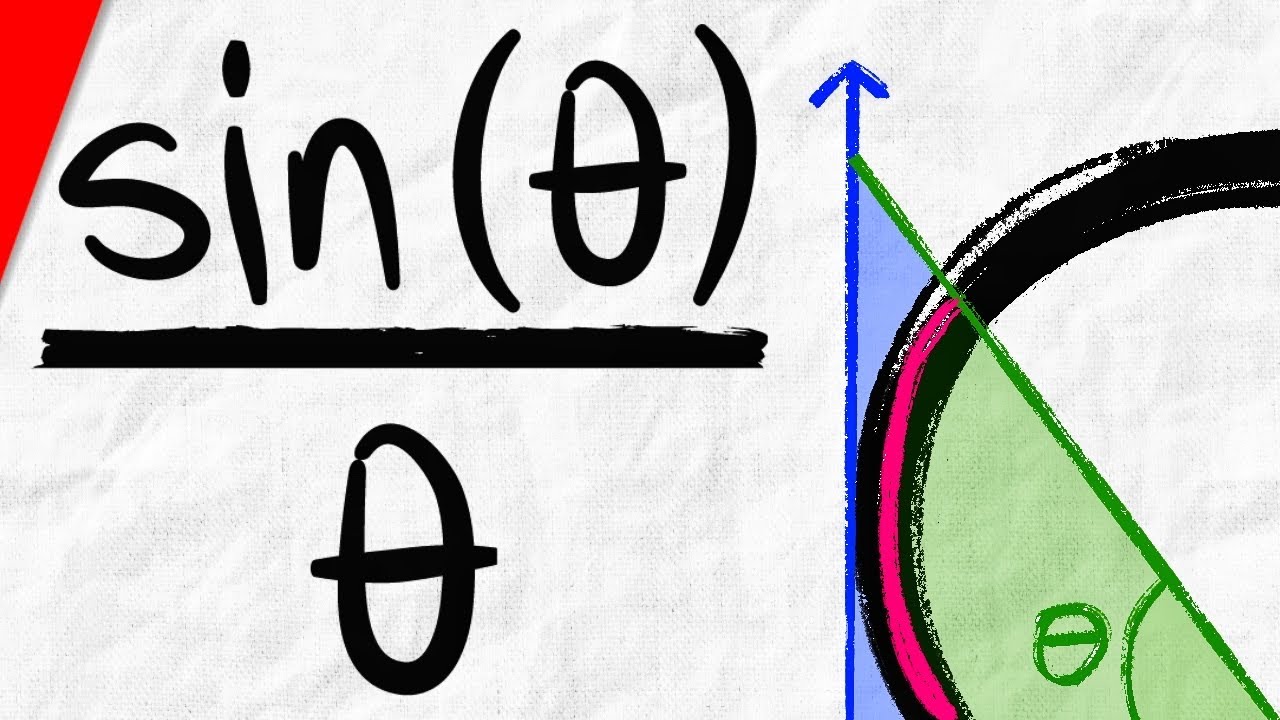
Показать описание

We prove the limit of sinx/x as x goes to 0 equals 1 using the squeeze theorem and a geometric argument involving sectors and triangles on the unit circle. #calculus1 #apcalculus

Join Wrath of Math to get exclusive videos, lecture notes, and more:

Squeeze Theorem Explained: (coming soon)

★DONATE★

Follow Wrath of Math on...

Рекомендации по теме

Комментарии

I studied Calculus some 50 years ago during my high school years and later heavily used it during my college time. Since graduation, I had not used it and so I had almost forgotten how to prove it using limit theory. Recently I wanted to teach my son on Calculus. So, I watched your video and found your explanation very easily to understand. Thank you.

samueltso

Best explanation on the internet of this theorem. Bravo, sir!😊

punditgi

nice explanation, I saw this in my calc textbook but this explains the steps very well

Scoutscout

What software are you using to write and annotate the explanation?

volaksin

2:23 For mnemonic purposes, I'm going to note that the area formula with *Sin* is the *Smallest, * while the one with *Tan is the Tallest.* 😅

surrealistidealist

But what if we will take the radius of the circle other than 1??

AbhishekKumar-dltf

Can you use the squeeze theorem to prove that the limit as x approaches 0 of (cos(x) - 1)/x is 0?

paulchapman

How do you prove that the tan area is larger than the sector area? Since the sector is curved?

maxyousofirahimi

I use hopital for the last problem. What are alternative approaches that we can use?

imbruno

Hey it's just a thought but we know sinx for very small values of x is similarly equal to x, right. Then the limit would be lim x-> 0 (x/x) . We can cancel out the x and get 1. Can this be a ideal solution though ?

daringd

Is there any proof for the order of areas?

darkl

limit((1-cos(x))/x, x=0) = limit((cos^2(x/2)+sin^2(x/2)-cos^2(x/2)+sin^2(x/2))/x, x=0)
=limit(2sin^2(x/2)/x, x=0)=limit(sin(x/2), x=0)*limit(sin(x/2)/(x/2), x=0)=0*1

holyshit

Great explanation as always...you have knowledge and talent to deliver informatiin...Respect from lebanon

mohfa

Finally a channel that uses the squeeze theorem correctly 😅

thexoxob

THE GREATEST VIDEO ON THE
THANK YOU SO MUCH SIR THIS WAS EXTREMELY HELPFUL

bug

Very nice, clear explanation, with simple, clear diagrams. Well done.

chrisrybak

Nicely done! It's been nearly four decades, but I'm pretty sure this is how I learned it from Apostol. (The book, not the man; he'd retired from teaching freshmen the year before.)

tomkerruish

loved the explanation, thanks a lot 🫠🤩🤩

ddarquesse

I finally understand this concept after watching this clear explanation ! Thank you.

christopherramsey

Making use of area to derive the inequality is circular reasoning.

yemoeaung

Proof: Limit of sinx/x as x approaches 0 with Squeeze Theorem | Calculus 1

Proof: Limit of sinx/x as x approaches 0 with Squeeze Theorem | Calculus 1

The most important limit in Calculus // Geometric Proof & Applications

Limit of sin(x)/x as x approaches 0 | Derivative rules | AP Calculus AB | Khan Academy

The Limit (do not use L'Hospital rule)

Proofs: Lim sinx/x =1 and lim [cosx -1] /x =0 as x goes to zero from geometry

Limit of sin(x)/x as x goes to Infinity (Squeeze Theorem) | Calculus 1 Exercises

Limit of sin(x)/x as x approaches 0 (Proof) | Derivative rules | Science Valhalla

02 Fundamental Limit of Trigonometric Function Proof sinx/x as x approaches zero

Limits: A proof of lim sinx/x =1

Limit of sinx/x as x approaches 0 (ILIEKMATHPHYSICS)

the most controversial limit in calculus 1

Proof that the Limit as x Approaches 0, sinx/x is 1 or lim x~0, sin(x)/x = 1

Pre-u: Prove [(sinx)/x]=1 when x is closest to 0

Visualizing the derivative of sin(x)

Master Trig Limits with sinx/x as x approaches 0 | Calculus 1 Exercises

Prove lim sin(x)/x = 1 as x approaches 0 (Squeeze Theorem)

This is a very famous limit

Proof: Limit of sinx/x as x approaches 0

Proof Lim (sinx)/x = 1 | Limits | Calculus

Limits of Trigonometric Functions

Proof of the derivative of sin(x) | Derivatives introduction | AP Calculus AB | Khan Academy

Limits Using Sinx/x =1

Limit of sinx/x^(1/3) as x approaches 0 | Calculus 1 Exercises

Proof of limit x goes to 0 of sinx/x is 1