filmov
tv
A Very Nice Exponential Equation | Best Solution To Exponential Challenge | Hints To Algebraic Maths

Показать описание
A Very Nice Exponential Equation/Best Solution To Exponential Challenge is a mathematical video you will ever love to watch because there are many tricks and hints you will definitely learn from this video clip.
In this video, I will show you how you can solve mathematical challenges of this kind without difficulties.
Watch from the beginning to the end without skipping any parts in order to get the full knowledge to solving this challenge and seminar mathematical challenges you will/may come across in the world of mathematics.
Also, do not forget to subscribe to this channel because we drop awesome videos that allow you to think outside the box and also enable you to match your mates and colleagues in the area of mathematics all around the world.
Welcome on board!!!
#onlinemathstv #challengingmathproblems
In this video, I will show you how you can solve mathematical challenges of this kind without difficulties.
Watch from the beginning to the end without skipping any parts in order to get the full knowledge to solving this challenge and seminar mathematical challenges you will/may come across in the world of mathematics.
Also, do not forget to subscribe to this channel because we drop awesome videos that allow you to think outside the box and also enable you to match your mates and colleagues in the area of mathematics all around the world.
Welcome on board!!!
#onlinemathstv #challengingmathproblems
A Very Nice Exponential Equation | Can you solve?
A Very Nice Exponential Equation | Two Methods
A Nice Exponential Equation | Math Olympiads
A Nice Exponential Equation | Math Olympiads
A Very Nice Exponential Equation | Math Olympiads
A Nice Exponential Equation
A Nice Exponential Equation
A Nice Math Olympiad Exponential Equation 3^x = X^9
Germany | A Nice Olympiad Exponential Problem | Olympiad Math Questions
A Nice Exponential Equation
A Nice Exponential Equation | A Special Function
A Super Nice Exponential Equation
A Nice Exponential Equation (5^x-3^x=16)
A Nice Exponential Equation | Math Olympiads
A Very Nice Exponential Equation | Math Olympiads
Solving A Nice Exponential Equation
A Nice Exponential Equation from SyberMath 😉
A Cool Exponential Equation | Algebra
A Nice Exponential Equation
Solving A Quick and Easy Exponential Equation
A Nice Exponential Equation
Solving A Nice Exponential Equation | Real and Complex
A Nice Homemade Exponential Equation
A Nice Exponential Equation
Комментарии
 0:09:21
0:09:21
 0:10:00
0:10:00
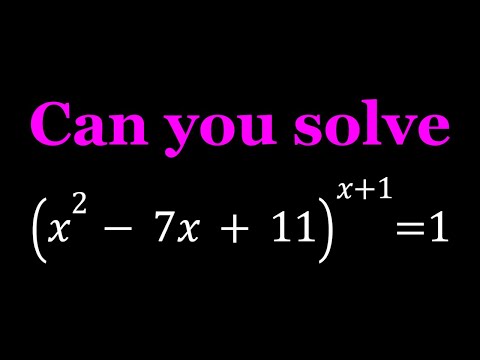 0:09:02
0:09:02
 0:08:21
0:08:21
 0:09:07
0:09:07
 0:09:32
0:09:32
 0:00:48
0:00:48
 0:02:34
0:02:34
 0:03:50
0:03:50
 0:08:18
0:08:18
 0:08:34
0:08:34
 0:07:39
0:07:39
 0:06:37
0:06:37
 0:06:50
0:06:50
 0:10:29
0:10:29
 0:09:56
0:09:56
 0:09:01
0:09:01
 0:00:25
0:00:25
 0:08:50
0:08:50
 0:00:28
0:00:28
 0:01:00
0:01:00
 0:10:28
0:10:28
 0:05:31
0:05:31
 0:04:33
0:04:33