filmov
tv
A Nice Exponential Equation | Math Olympiads
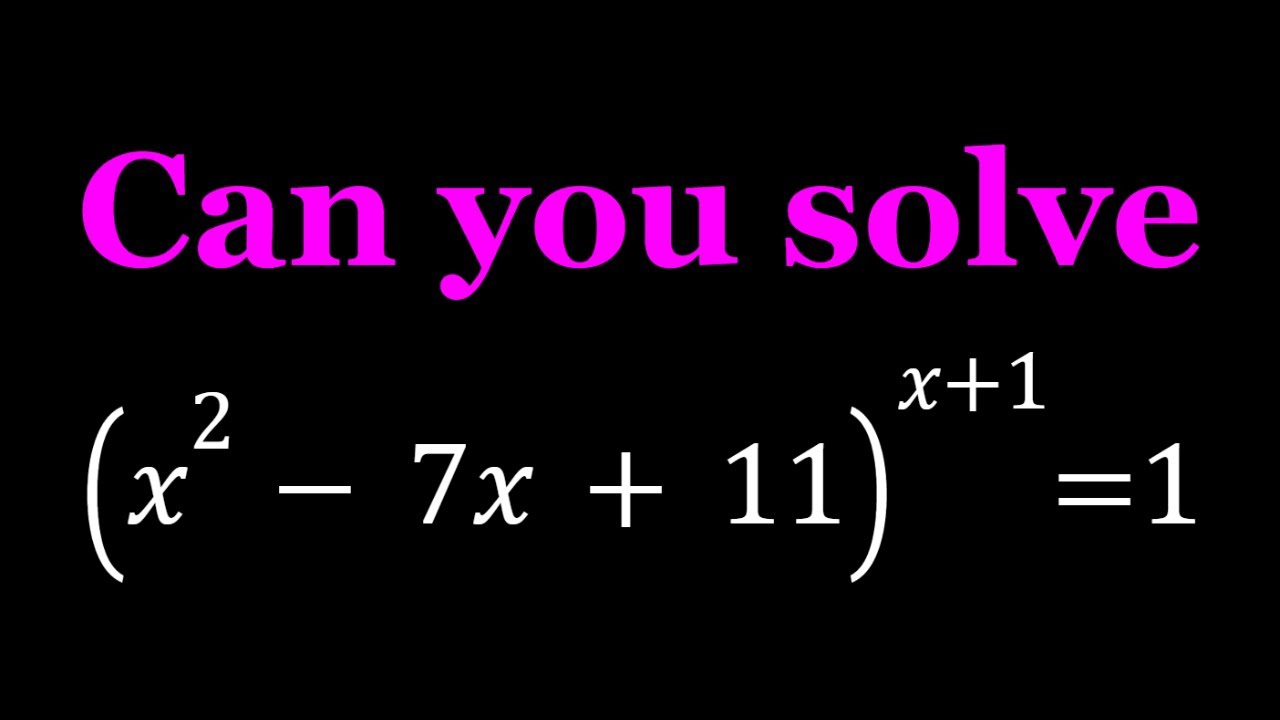
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
(x^2-7x+11)^(x+1)=1
#ChallengingMathProblems #ExponentialEquations #Exponentials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
SIMILAR PROBLEMS 🤩
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
(x^2-7x+11)^(x+1)=1
#ChallengingMathProblems #ExponentialEquations #Exponentials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
SIMILAR PROBLEMS 🤩
PLAYLISTS 🎵 :
A Nice Exponential Equation (5^x-3^x=16)
A Nice Math Olympiad Exponential Equation 3^x = X^9
A Nice Exponential Equation
A Nice Exponential Equation, x²=2ˣ
A Nice Math Olympiad Exponential Equation 8^x = X^32
A Nice Exponential Equation | Math Olympiads
A Very Nice Exponential Equation | Can you solve?
United Kingdom - A Nice Exponential Equation | Math olympiad Question
how to solve this exponential problem? A nice Exponential equation @mathscuriosity494
Solving Exponential Equations
A Nice Exponential Equation #algebra
A Nice Exponential Equation
A Nice Exponential Equation | Can you solve this? | Algebra Simplification Problem
A Nice Exponential Equation (e^x=x^e)
A Nice Exponential Equation | Math Olympiads
Nice exponential equation || Dare to solve x? Olympiad math exponential equation
A Nice Exponential Equation from SyberMath 😉
A Nice Exponential Equation
A Nice Exponential Equation?
A Nice Exponential Equation from Romania
A nice exponential equation
Solving A Nice Exponential Equation | Real and Complex
Solving A Nice Exponential Equation
Solving Exponential Equation
Комментарии
 0:06:37
0:06:37
 0:02:34
0:02:34
 0:09:32
0:09:32
 0:10:34
0:10:34
 0:03:12
0:03:12
 0:08:21
0:08:21
 0:09:21
0:09:21
 0:09:19
0:09:19
 0:07:54
0:07:54
 0:16:36
0:16:36
 0:06:43
0:06:43
 0:08:50
0:08:50
 0:06:06
0:06:06
 0:09:59
0:09:59
 0:06:50
0:06:50
 0:02:22
0:02:22
 0:09:01
0:09:01
 0:04:33
0:04:33
 0:03:41
0:03:41
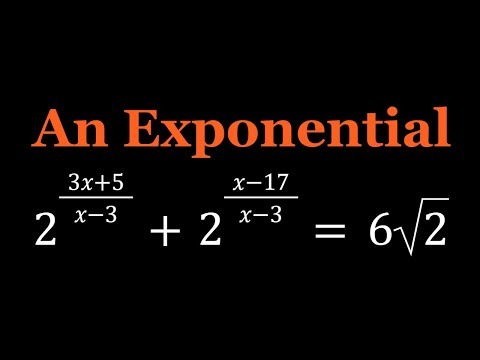 0:10:27
0:10:27
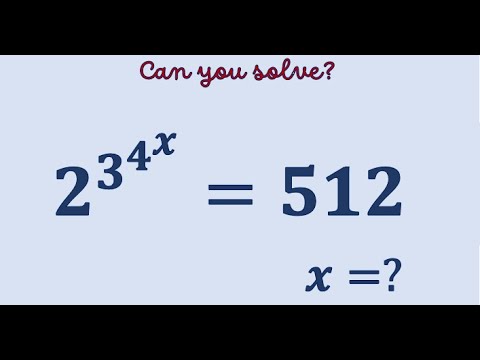 0:01:10
0:01:10
 0:10:28
0:10:28
 0:09:56
0:09:56
 0:00:56
0:00:56