filmov
tv
A Very Nice Exponential Equation | Math Olympiads

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
x^x=2^{3x+192}
#ChallengingMathProblems #ExponentialEquations
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
x^x=2^{3x+192}
#ChallengingMathProblems #ExponentialEquations
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
A Very Nice Exponential Equation | Math Olympiads
USA Nice Olympiad Exponential Equation: solve for a!
SOLVE FOR X, A VERY NICE EXPONENTIAL EQUATION
A Very Nice Exponential Equation | Can you solve?
A Nice Exponential Equation
A Nice Math Olympiad Exponential Equation 3^x = X^9
A Very Nice Exponential Equation | Two Methods
Solving A Nice Exponential Equation
Solving A Homemade Exponential Equation
Another Nice Exponential Equation
A nice exponential equation.
A Very Nice Exponential Equation | Best Solution To Exponential Challenge | Hints To Algebraic Maths
A Nice Exponential Equation, x²=2ˣ
A Very Nice Exponential Equation | What Most Mathematicians Try to Hide
A Nice Exponential Equation (5^x-3^x=16)
A Very Nice Exponential Equation For Math Geniuses || India Math Lovers Only Can Solve This.
A Very Nice Exponential Equation | Math Olympiads
A Nice Exponential Equation
A Nice Exponential Equation | Math Olympiads
An Interesting Exponential Equation
British | A very nice exponential equation | Math Olympiad question |
A Nice Exponential Equation from Romania
Switzerland | A very nice exponential equation | Math Olympiad question |
United Kingdom - A Nice Exponential Equation | Math olympiad Question
Комментарии
 0:09:07
0:09:07
 0:08:05
0:08:05
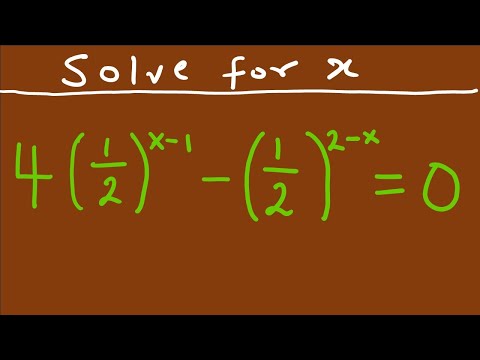 0:02:52
0:02:52
 0:09:21
0:09:21
 0:09:32
0:09:32
 0:02:34
0:02:34
 0:10:00
0:10:00
 0:06:30
0:06:30
 0:08:46
0:08:46
 0:09:21
0:09:21
 0:00:55
0:00:55
 0:19:12
0:19:12
 0:10:34
0:10:34
 0:05:05
0:05:05
 0:06:37
0:06:37
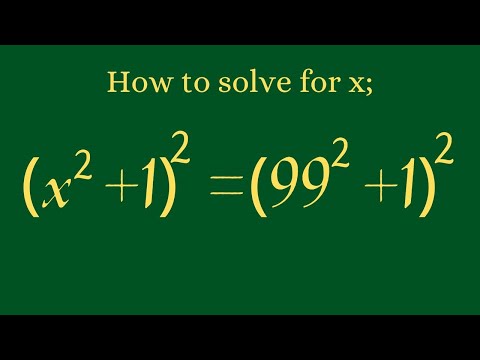 0:12:07
0:12:07
 0:10:29
0:10:29
 0:08:50
0:08:50
 0:08:21
0:08:21
 0:08:40
0:08:40
 0:06:05
0:06:05
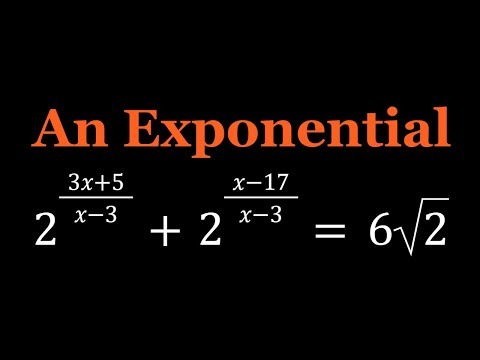 0:10:27
0:10:27
 0:06:19
0:06:19
 0:09:19
0:09:19