filmov
tv
Math Olympiad Question | Nice Algebra Equation | You should know this trick!!

Показать описание
Thailand | Math Olympiad Question | Nice Algebra Equation
Mexico - A Nice Math Olympiad Exponential Problem
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
Norway Math Olympiad Question | You should be able to solve this!
Math Olympiad Question | Nice Algebra Equation | You should know this trick!!
A Nice Math Olympiad Exponential Equation 3^x = X^9
A nice math Olympiad question #math #matholympiad
Japanese Math Olympiad Problem | A Nice Math Problem : Comparison
How to solve this nice math algebra problem | Olympiad Question
A nice math problem to solve| Solve for x and y#maths #matholympiad
A nice math Olympiad question #maths #matheolympiad
United Kingdom - A Nice Exponential Equation | Math olympiad Question
France - Math Olympiad Question | An Algebraic Expression | You should be able to solve this!
Luxembourg - Math Olympiad Question | You should know this trick
A nice exponential equation to solve| Math Olympiad #maths #matheolympiad
A Nice math Olympiad simplification #olympiad #mathematics #maths #exponents #logarithm #usastudy
Math Olympiad Question | You should know this trick!!
A nice math Olympiad problem| Solve for x#maths #matholympiad
A nice Olympiad qualifying question from the Philippines
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
A nice math Olympiad problem |you should try to solve this#math #matholympiad
A Nice Factorial Math Olympiad Problem | Find the value of n ?
Korean Math Olympiad Question | A Nice Exponential Problem
China | Math Olympiad | A Nice Algebra Problem 👇
Комментарии
 0:01:26
0:01:26
 0:08:36
0:08:36
 0:01:54
0:01:54
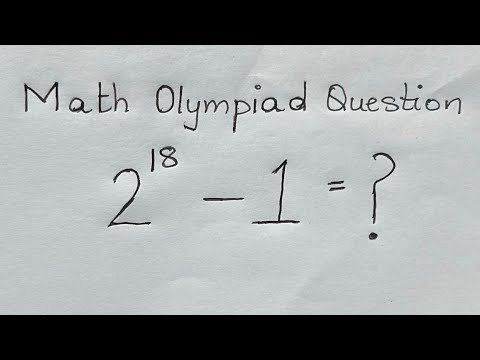 0:03:21
0:03:21
 0:07:26
0:07:26
 0:02:34
0:02:34
 0:07:53
0:07:53
 0:04:15
0:04:15
 0:05:29
0:05:29
 0:05:39
0:05:39
 0:13:24
0:13:24
 0:09:19
0:09:19
 0:08:40
0:08:40
 0:02:51
0:02:51
 0:04:55
0:04:55
 0:00:54
0:00:54
 0:00:33
0:00:33
 0:04:21
0:04:21
 0:06:53
0:06:53
 0:00:52
0:00:52
 0:16:39
0:16:39
 0:02:39
0:02:39
 0:03:15
0:03:15
 0:10:37
0:10:37