filmov
tv
France - Math Olympiad Question | An Algebraic Expression | You should be able to solve this!

Показать описание
Maths Olympiads are held all around the world to recognise students who excel in maths. The test is offered at many grade levels and provides them with numerous possibilities to win certifications, awards, and even scholarships for higher studies.
France - Math Olympiad Question | An Algebraic Expression | You should be able to solve this!
France| A nice math Olympiad question #maths #matholympiad
France - Math Olympiad Question
France - Math Olympiad Question | Be Careful!
France - Math Olympiad Question | An Algebraic Expression | You should be able to solve this!
Math Olympiad Question | (France)
Solve for positive integer solutions| Math Olympiad #maths #matholympiad
France - Math Olympiad Problem
France - Math Olympiad Question | An Algebraic Expression | You should be able to solve this!
France | math olympiad question | Can you solve this
France| Math Olympiad question #math#matholympiad
France Math Olympiad Question | Can you Solve this ?
Luxembourg - Math Olympiad Question | You should know this trick
Many could not solve this France Math Olympiad Question! Can you?
France - Maths Olympiad Question
France - Math Olympiad Question | Bulgarian - Math Olympiad Question | International Math Olympiad
France Math Olympiad Question | You should know this trick!
France | Math Olympiad Question | An Algebra Expiration | You should know this Solotion |
FRANCE - Math Olympiad Question. Learn This Math Tricks.
United Kingdom - A Nice Exponential Equation | Math olympiad Question
France Math Olympiad Question / A Key Trick You Must Know.
France Math Olympiad Question | An interesting question
A nice math Olympiad question| Solve for x#maths #olympiad
Can you solve? A nice math problem to solve #maths #mathematics
Комментарии
 0:08:40
0:08:40
 0:08:48
0:08:48
 0:04:00
0:04:00
 0:15:49
0:15:49
 0:07:34
0:07:34
 0:09:03
0:09:03
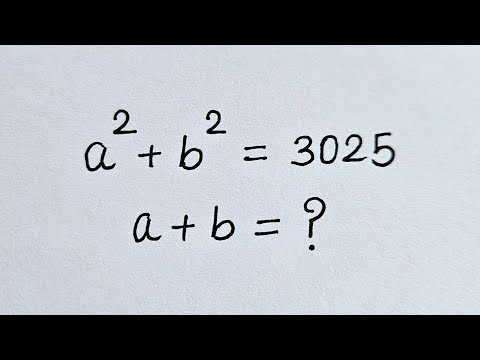 0:09:49
0:09:49
 0:05:03
0:05:03
 0:03:33
0:03:33
 0:03:23
0:03:23
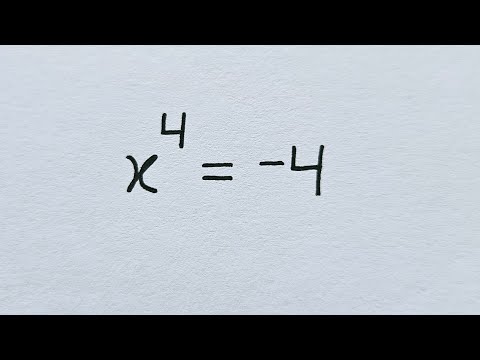 0:10:23
0:10:23
 0:02:56
0:02:56
 0:02:51
0:02:51
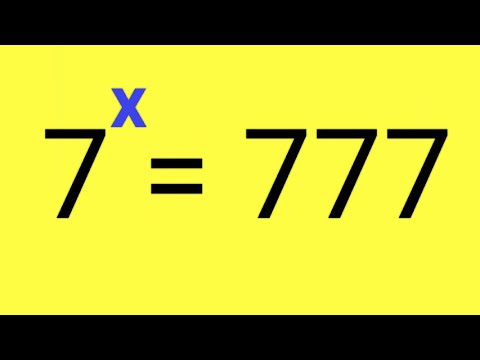 0:05:11
0:05:11
 0:04:58
0:04:58
 0:13:13
0:13:13
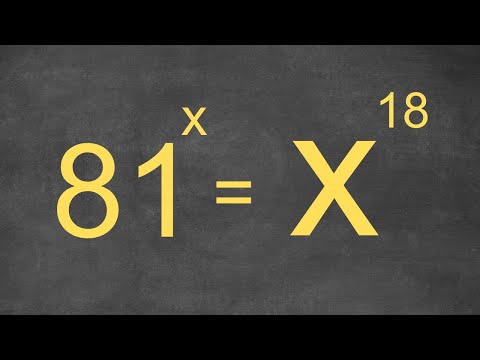 0:04:02
0:04:02
 0:09:17
0:09:17
 0:08:48
0:08:48
 0:09:19
0:09:19
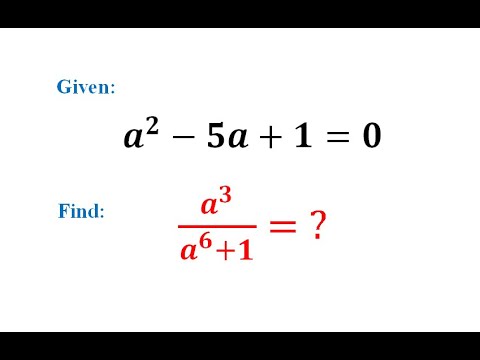 0:04:04
0:04:04
 0:05:44
0:05:44
 0:08:20
0:08:20
 0:05:24
0:05:24