filmov
tv
Introduction to the Black-Scholes formula (BSM)
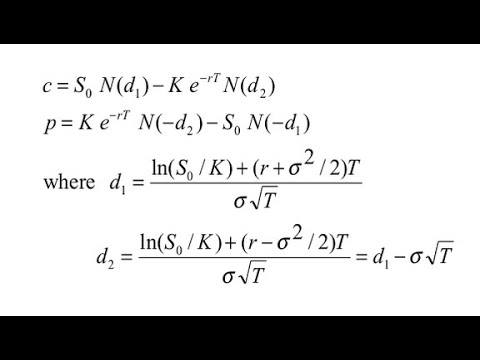
Показать описание
Black-Scholes option pricing model (its Merton’s extension that accounts for dividends), there are six parameters which affect option prices:
Do like ,share ,comment && Subscribe for more such videos!!!
So = underlying price ($$$ per share)
X = strike price ($$$ per share)
σ = volatility (% p.a.)
r = continuously compounded risk-free interest rate (% p.a.)
q = continuously compounded dividend yield (% p.a.)
t = time to expiration (% of year)
Value of call option = So * ND1 - K *e^-rt * ND2
Value of put option = K * e^-rt* ND2 - So* ND1
Calculation of ND1 & ND2 in case of call option
D1 = [ ln(So/K) + (r + ∂ ^ 2 / 2) * t ] / [ ∂ * sqrt (t) ]
D2 = [ ln(So/K) + (r - ∂ ^ 2 / 2) * t ] / [ ∂ * sqrt (t) ]
Normal Distribution formal in spreadsheet = normsdist(d1), normsdist(d2)
For put option use "-" in normsdist(-d1) or normsdist(-d2)
#conceptbuilders #Nirajbotadra #Valuation
Do like ,share ,comment && Subscribe for more such videos!!!
So = underlying price ($$$ per share)
X = strike price ($$$ per share)
σ = volatility (% p.a.)
r = continuously compounded risk-free interest rate (% p.a.)
q = continuously compounded dividend yield (% p.a.)
t = time to expiration (% of year)
Value of call option = So * ND1 - K *e^-rt * ND2
Value of put option = K * e^-rt* ND2 - So* ND1
Calculation of ND1 & ND2 in case of call option
D1 = [ ln(So/K) + (r + ∂ ^ 2 / 2) * t ] / [ ∂ * sqrt (t) ]
D2 = [ ln(So/K) + (r - ∂ ^ 2 / 2) * t ] / [ ∂ * sqrt (t) ]
Normal Distribution formal in spreadsheet = normsdist(d1), normsdist(d2)
For put option use "-" in normsdist(-d1) or normsdist(-d2)
#conceptbuilders #Nirajbotadra #Valuation
0:10:24
Introduction to the Black-Scholes formula | Finance & Capital Markets | Khan Academy
0:14:03
Black Scholes Explained - A Mathematical Breakdown
0:03:40
Black Scholes Formula explained simply
0:15:54
Warren Buffett: Black-Scholes Formula Is Total Nonsense
Introduction to the Black-Scholes formula (BSM)
0:00:39
Charlie Munger on Black–Scholes
0:10:40
The Black-Scholes Model EXPLAINED
0:05:48
An intuitive explanation the Black Scholes' formula
0:09:23
Black Scholes Option Pricing Model Explained In Excel
0:08:29
Is the Black Scholes Actually Used in the Real World
0:00:59
Mastering the Black-Scholes Model: Essential Knowledge for Options Traders
0:31:46
Introduction to Black-Scholes
0:10:24
Introduction to the Black Scholes Formula
0:05:55
Black Scholes Model | What ist the Black Scholes Formula? | explained
0:05:52
The Black-Scholes Formula Explained
0:49:52
19. Black-Scholes Formula, Risk-neutral Valuation
0:09:53
The Easiest Way to Derive the Black-Scholes Model
0:13:39
Black-Scholes Option Pricing Model -- Intro and Call Example
0:10:51
Black Scholes Option Pricing Model
0:00:59
Unlocking the Black-Scholes Model: Visualizing the Power of Options Trading in 60 Seconds
0:04:20
What is the Black Scholes Model
0:05:00
Implied volatility | Finance & Capital Markets | Khan Academy
0:00:34
Did you ever use the Black-Scholes model, aka the Black-Scholes-Merton (BSM) model? #shorts
0:09:43
Introduction to the Black Scholes Model
Комментарии