filmov
tv
Least Squares

Показать описание
In this video, I solve linear systems equations that are unsolvable (whoa!!!). More precisely, I show how to solve the systems using the least-squares method, first by doing it the Peyam way using orthogonal projections, and then by using the classical way (by multiplying by A^T). Finally, I show why the two methods are equivalent. Along the way, I also talk about the QR decomposition of a matrix. Enjoy!
What is Least Squares?
Linear Regression Using Least Squares Method - Line of Best Fit Equation
Least squares approximation | Linear Algebra | Khan Academy
Introduction to residuals and least squares regression
Least squares using matrices | Lecture 26 | Matrix Algebra for Engineers
The Least Squares Formula: A Derivation
Linear Least Squares to Solve Nonlinear Problems
How to calculate linear regression using least square method
Statistics: Least Square Regression Grade 12 Prelim 2024 Gauteng Province
Least Squares - 5 Minutes with Cyrill
Least Squares Approximations
Least Squares Approximation
9. Four Ways to Solve Least Squares Problems
Deriving the least squares estimators of the slope and intercept (simple linear regression)
Least Squares Approximation
Least Squares
Simple Linear Regression: The Least Squares Regression Line
Linear Systems of Equations, Least Squares Regression, Pseudoinverse
Determine a Least Squares Solutions to Ax=b
Linear Regression, Clearly Explained!!!
Least squares line (KristaKingMath)
What is Least Squares Estimation?
Ordinary Least Squares regression or Linear regression
Introduction To Ordinary Least Squares With Examples
Комментарии
 0:02:43
0:02:43
 0:15:05
0:15:05
 0:15:32
0:15:32
 0:07:39
0:07:39
 0:10:15
0:10:15
 0:10:31
0:10:31
 0:12:27
0:12:27
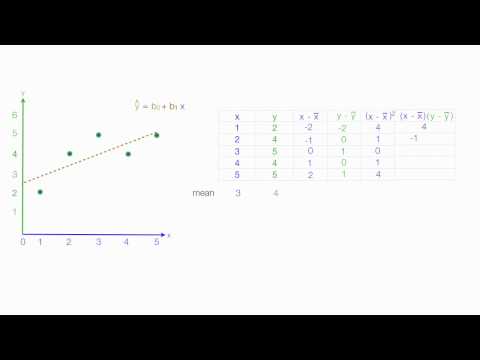 0:08:29
0:08:29
 0:08:48
0:08:48
 0:05:18
0:05:18
 0:07:28
0:07:28
 0:07:52
0:07:52
 0:49:51
0:49:51
 0:12:13
0:12:13
 0:08:04
0:08:04
 0:29:01
0:29:01
 0:07:24
0:07:24
 0:11:53
0:11:53
 0:06:28
0:06:28
 0:27:27
0:27:27
 0:07:47
0:07:47
 0:14:31
0:14:31
 0:02:10
0:02:10
 0:03:34
0:03:34