filmov
tv
Linear Systems of Equations, Least Squares Regression, Pseudoinverse

Показать описание
This video describes how the SVD can be used to solve linear systems of equations. In particular, it is possible to solve nonsquare systems (overdetermined or underdetermined) via least squares regression and the pseudoinverse.
These lectures follow Chapter 1 from: "Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control" by Brunton and Kutz
This video was produced at the University of Washington
These lectures follow Chapter 1 from: "Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control" by Brunton and Kutz
This video was produced at the University of Washington
Linear Systems of Equations, Least Squares Regression, Pseudoinverse
Least squares using matrices | Lecture 26 | Matrix Algebra for Engineers
LEAST SQUARE SOLUTIONS FOR SYSTEM OF EQUATIONS
1.5 - Solution Sets of Linear Systems
Least squares approximation | Linear Algebra | Khan Academy
Overdetermined System of Equations | Ch. 2, Linear Regression
Consistency of a System of Linear Equations
How do we solve a system of linear equations using any method
Linear Algebra: number systems, overview of matrix math, 8-19-24
Least Squares Regression and the SVD
Linear equations, Least squares solutions and Linear regression
Newton and Gauss-Newton methods for nonlinear system of equations and least squares problem
Least Square Solution of a Given System of Linear equations
Linear Systems of Equations, Ax=b
Linear Regression Using Least Squares Method - Line of Best Fit Equation
Solving Systems of Equations With 3 Variables & Word Problems
Nonlinear Least Squares
The normal equations
Elimination Method For Solving Systems of Linear Equations Using Addition and Multiplication, Algebr
20. Python to solve for systems of linear equations
Foundations & Pre-Calc 10 Lesson 7.1 'Systems of Linear Equations'
Linear Equations - Algebra
1.1 Systems of Linear Equations
Least squares examples | Alternate coordinate systems (bases) | Linear Algebra | Khan Academy
Комментарии
 0:11:53
0:11:53
 0:10:15
0:10:15
 0:04:58
0:04:58
 0:22:06
0:22:06
 0:15:32
0:15:32
 0:03:47
0:03:47
 0:03:11
0:03:11
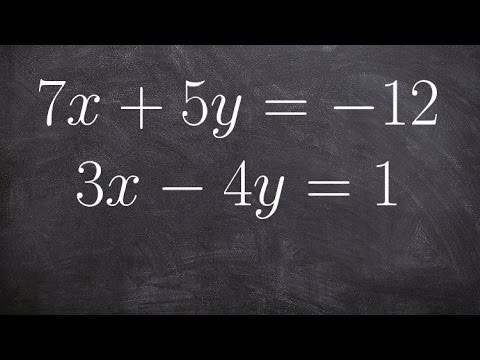 0:04:34
0:04:34
 0:46:13
0:46:13
 0:05:43
0:05:43
 0:26:22
0:26:22
 0:07:30
0:07:30
 0:28:25
0:28:25
 0:10:04
0:10:04
 0:15:05
0:15:05
 0:12:44
0:12:44
 0:10:56
0:10:56
 0:09:36
0:09:36
 0:10:21
0:10:21
 0:05:53
0:05:53
 0:15:51
0:15:51
 0:32:05
0:32:05
 0:18:49
0:18:49
 0:18:50
0:18:50