filmov
tv
Персидская олимпиадная задача по математике

Показать описание
(a⁸ - a²)/(a⁴ - a²) = 9
Персидская олимпиадная задача по математике
Основы математики | Задача из норвежской олимпиады 8 класса...
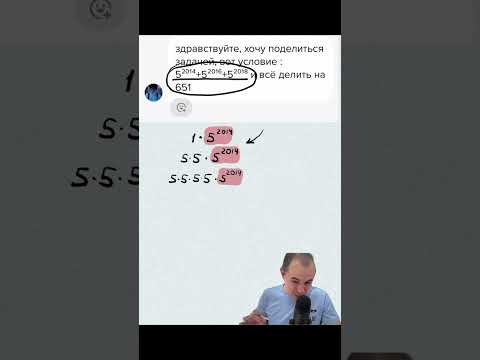
ОЛИМПИАДная задача в ОДНО действие
ПЕРСИДСКАЯ ОЛИМПИАДА 😉 #егэ #математика #профильныйегэ #shorts #огэ...
Олимпиадная задача со степенями #математика #арифметика #дробь #степень #олимпиада...
Разбор самой простой задачи международной олимпиады по математике...
Как решать олимпиадные задачи?
Задача с американской олимпиады, которую никто не решил....
Американская математическая олимпиада. #математика #олимпиада #уравнение #степень #логарифмы...
Олимпиадная задача для 5 класса
Олимпиадная задача, которую смогли решить единицы
Задача из курса олимпиадная математика #репетитор #математика #олимпиада #логика...
Хитрая задача из американской математической олимпиады Проверь свои знания!...
Советская олимпиада, которую сегодня решить только 2% школьников...
Как решать олимпиадные задачи-ловушки про лифт?
@Задача Олимпиады Турция (Х-У) максимум найти #математика...
Олимпиадная Математика в РШШ
Задача с чешской олимпиады, которую решили только 14% школьников...
Олимпиадная задача, которую смогли решить единицы
Уравнение из областной олимпиады #математика #репетитор #репетитор...
Задача по олимпиаде по математике за 3 класс решить?
Олимпиадная задача: какой сегодня день недели? Попробуйте решить | Математика...
Олимпиадная математика для 1 классов
Классная задача на логику из олимпиады 7 класса
Комментарии
 0:05:52
0:05:52
 0:02:13
0:02:13
 0:00:52
0:00:52
 0:00:59
0:00:59
 0:01:01
0:01:01
 0:12:47
0:12:47
 0:14:48
0:14:48
 0:03:26
0:03:26
 0:00:57
0:00:57
 0:02:02
0:02:02
 0:02:12
0:02:12
 0:01:00
0:01:00
 0:00:59
0:00:59
 0:04:13
0:04:13
 0:00:49
0:00:49
 0:00:10
0:00:10
 0:00:21
0:00:21
 0:04:38
0:04:38
 0:04:37
0:04:37
 0:00:58
0:00:58
 0:00:45
0:00:45
 0:01:00
0:01:00
 0:00:11
0:00:11
 0:02:01
0:02:01