filmov
tv
Lagrange multipliers in three dimensions with two constraints (KristaKingMath)
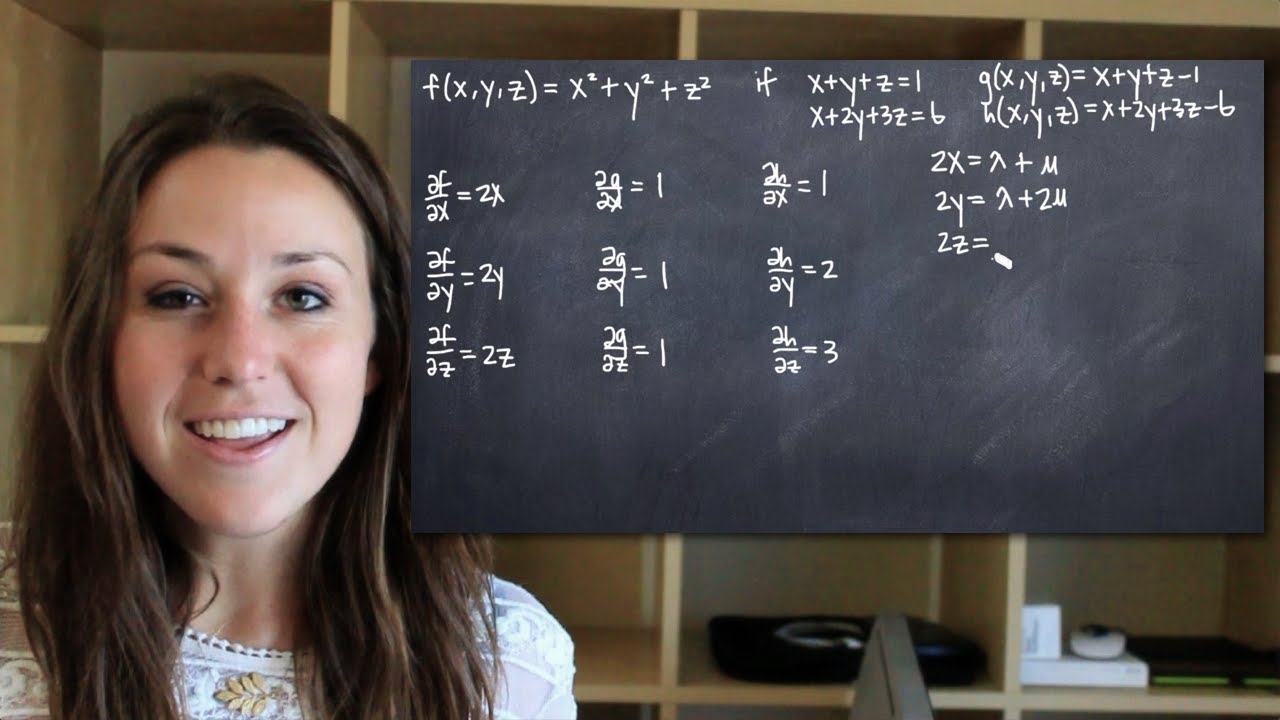
Показать описание
Learn how to use Lagrange multipliers to find the extrema of a three-dimensional function, given two constraint functions. In order to complete this problem, you'll need to take partial derivatives of the original function, as well as each of the constraint functions. Then, you'll set up your equations in order to solve for two multipliers and the three variables from the original function. Once you've found values for the original variables, you'll plug those values into the original function. This will give you the value of a maximum or minimum of the function.
● ● ● GET EXTRA HELP ● ● ●
● ● ● CONNECT WITH KRISTA ● ● ●
Hi, I’m Krista! I make math courses to keep you from banging your head against the wall. ;)
Math class was always so frustrating for me. I’d go to a class, spend hours on homework, and three days later have an “Ah-ha!” moment about how the problems worked that could have slashed my homework time in half. I’d think, “WHY didn’t my teacher just tell me this in the first place?!”
Комментарии
 0:12:24
0:12:24
 0:08:33
0:08:33
 0:06:10
0:06:10
 0:13:18
0:13:18
 0:08:43
0:08:43
 0:33:46
0:33:46
 0:14:54
0:14:54
 0:13:40
0:13:40
 0:58:33
0:58:33
 0:13:01
0:13:01
 0:36:00
0:36:00
 0:16:29
0:16:29
 0:08:49
0:08:49
 0:17:09
0:17:09
 0:09:11
0:09:11
 0:17:57
0:17:57
 0:14:24
0:14:24
 0:15:53
0:15:53
 0:12:33
0:12:33
 0:28:08
0:28:08
 0:11:24
0:11:24
 0:10:24
0:10:24
 0:10:18
0:10:18
 0:06:29
0:06:29