Lagrange Multipliers | Geometric Meaning & Full Example

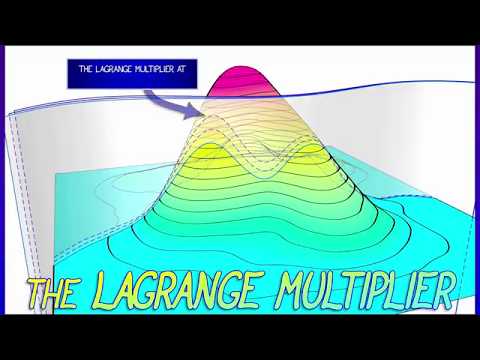
Lagrange Multipliers solve constrained optimization problems. That is, it is a technique for finding maximum or minimum values of a function subject to some constraint, like finding the highest point on a mountain subject to the fact you can only walk along a trail. In this video we study the contour lines or level curves of a function and see geometrically why they are maximized when they are tangent to the constraint curve. That tangency condition leads to the algebraic formula that the gradient of f is equal to lambda times the gradient of g. In this video we will visualize the geometric meaning and then walk through a concrete example.

****************************************************
YOUR TURN! Learning math requires more than just watching videos, so make sure you reflect, ask questions, and do lots of practice problems!
****************************************************

****************************************************
Other Course Playlists:

***************************************************

► Want to learn math effectively? Check out my "Learning Math" Series:

►Want some cool math? Check out my "Cool Math" Series:

****************************************************

*****************************************************

This video was created by Dr. Trefor Bazett. I'm an Assistant Teaching Professor at the University of Victoria.

BECOME A MEMBER:

MATH BOOKS & MERCH I LOVE:

[BloobleBonker]

At the age of 66 after trying to understand Lagrange multipliers since the age of 18, I think I've finally got it. Conturs and gradients. Excellent graphics!

[gamingmonts]

by just seeing that graph, I immidiently understood something my professor talked about for 2 freakin hours 😂

[nathanborak]

This is not the way I have usually thought about it but it's equivalent. The way I've usually thought about it is that you imagine walking along the constraint and observing the gradient of f as you go. If the gradient of f has any component along the constraint, it means you can keep walking along the constraint and get higher (or lower) values of f, since the directional derivative is just the component of gradf(f) along the direction you're moving. Therefor you keep walking around the constraint until you reach a point where the gradient of f is normal to the constraint, since at this point f is instantaneously not changing. To me this is more intuitive than thinking the level curve of f should be tangent to the constraint, even though the gradient of f being normal to the constraint IS the level curve being tangent to it. Different strokes I guess.

[xiadanji]

Mr. Bazett, I think this version of explanation is the best one in whole Youtube, thank you very much!!!

[Aruuuq]

Such a nice video. Very enthusiastic presentation. The graphics are some of the most explanatory one for Lagrangian Multipliers that I've ever seen.

[shemsnow]

I think you're the first person I've ever heard explain math without either focusing too much on precise definitions and proofs that no one cares about or just expecting us to memorize formulas. Nice step by step relevant instructions. Very nice.

[tedskins]

Thank you very much. I find that geometric interpretations of math concepts often make it significantly easier for me to understand

[brucemurdock]

The internet is a blessing, because of people like you

[mathematicaljulian]

Taking multivariable calculus right now and I can’t stand when I have a lecture that is super long for absolutely no reason without even taking the time to explain some intuition. This video is great for the intuition thank you

[ayushthada]

I feel whenever I need to brush up on my knowledge of calculus, I always end up on your channel. Your channel is a great learning resource. Thanks for posting these videos. Wish you were teaching Differential Geometry of Manifolds.

[abhinavsharma]

Every person who has ever taken an optimization course should see this short video! It gives you so much mathematical intuition to the concept of constraints and Lagrange multipliers!

[Stan-san]

I saw this 9 years ago in university and needed a refresher, this is amazingly well explained.

[kasyapdharanikota]

best professor teaching maths, great explanation, very thankful to you

[borannchanrathnak]

Thanks for your explanation, Dr. Trefor Bazett. I was trying to imagine the stuffs in my head and it didn't work until I came here to see your graph visualization. Thumb up for your great work.

[jrt]

Thank you so much, this is on my entrance exam to Japanese University

[lewiduressa]

Your videos are helping me understand my Calc 3 class concept, and you explain it way better than my teacher. Thank you!!

[muhahaha]

i already passed my analysis 2 exam but i never understood what i was doing when using langrange multipliers, i just learnt how to use it. Now i finally understand what i have been doing all the time thx

[mushfiqurrahman]

Your explanation is really excellent ever i see on multi variable calculus....may Allah increase your knowledge more

[suheladesilva]

Brilliant Dr. Trevor, thanks a lot for your excellent explanation.

[everelement]

Man, this video deserves more views and likes. I definitely need these 3D graph to understand it.