filmov
tv
Proof: Cosets are Disjoint and Equal Size
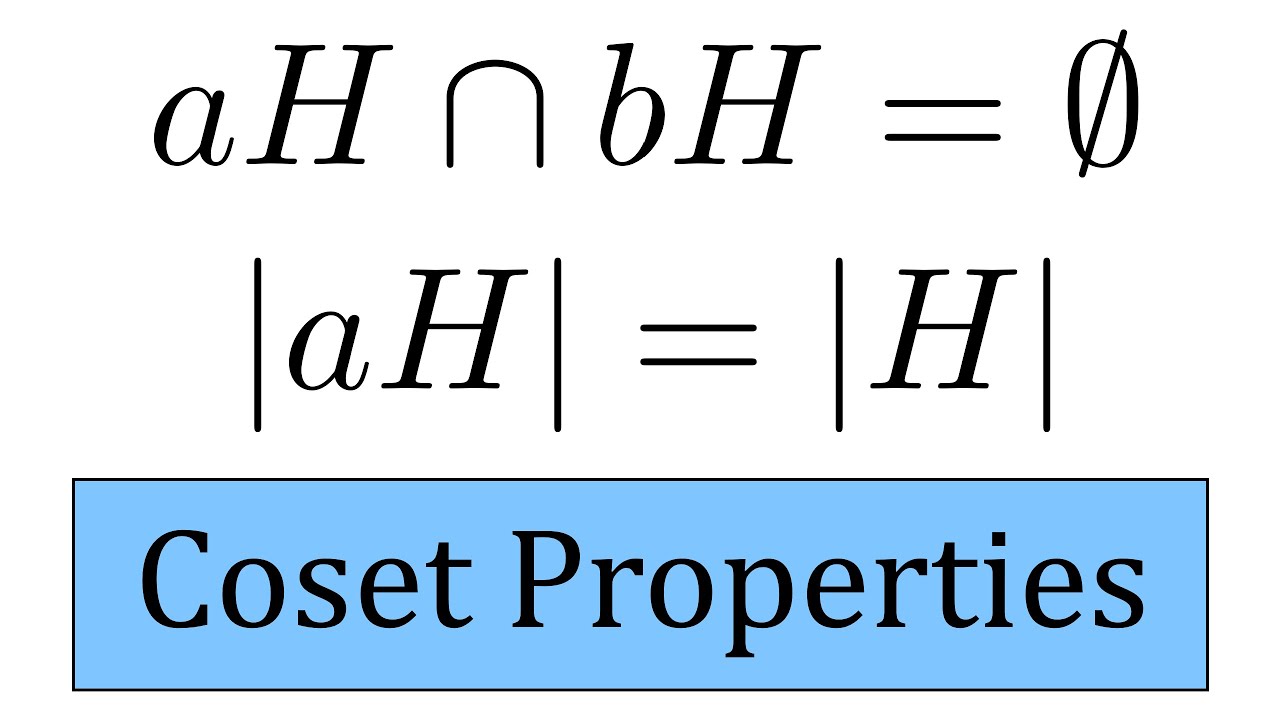
Показать описание
Explanation for why cosets of a subgroup are either equal or disjoint and why all cosets have the same size.
0:00 Cosets are disjoint
3:15 Cosets have same size
Subscribe to see more new math videos!
Music: C418 - Pr Department
0:00 Cosets are disjoint
3:15 Cosets have same size
Subscribe to see more new math videos!
Music: C418 - Pr Department
Proof: Cosets are Disjoint and Equal Size
Cosets in Group Theory | Abstract Algebra
Proof: Cosets Partition the Group | Abstract Algebra
Any two right(left) Cosets are either disjoint or Identical.
Any two right(left) cosets are either disjoint or identical | coset are either disjoint or equal
Any two Rights Cosets( or Left Cosets) are either disjoint or identical I COSETS I RTMNU BSC MATHS I
Group theory, prove that any two right cosets are either disjoint or identical
Either two cosets are equal or disjoint
Group Theory 23: Cosets are either disjoint or equal
2 bsc mathematics costs, any two left cosets of H are either disjoint or identical
Group Theory 25: All cosets are the same size
Abstract Algebra 39: A proof of Lagrange's theorem
Cosets. Lagrange's theorem
Two Properties of Cosets | Abstract Algebra
Cosets are either disjoint or equal - Group Theory
Visual Group Theory, Lecture 3.2: Cosets
Abstract Algebra 7.3: Properties of Cosets
17 When are two left cosets equal
Two right(left) cosets of subgroup are either identical or disjoint.
Group theory : cosets are either identical or disjoint
Any two right cosets of a subgroup H of a group G are either disjoint or identical
Coset as an Equivalence Class - Chapter 5 - Lecture 9
Any two right(left) cosets of subgroups are either disjoint or identical
Any two left cosets are either identical or disjoint # Algebraic structures # TAM5A
Комментарии
 0:04:46
0:04:46
 0:15:26
0:15:26
 0:06:31
0:06:31
 0:06:02
0:06:02
 0:07:39
0:07:39
 0:09:30
0:09:30
 0:09:11
0:09:11
 0:04:53
0:04:53
 0:02:48
0:02:48
 0:05:00
0:05:00
 0:03:03
0:03:03
 0:09:52
0:09:52
 0:32:21
0:32:21
 0:05:18
0:05:18
 0:05:56
0:05:56
 0:19:11
0:19:11
 0:04:57
0:04:57
 0:13:53
0:13:53
 0:06:21
0:06:21
 0:12:09
0:12:09
 0:08:25
0:08:25
 0:13:02
0:13:02
 0:09:23
0:09:23
 0:10:34
0:10:34