filmov
tv
Solving a Logarithmic Exponential Equation
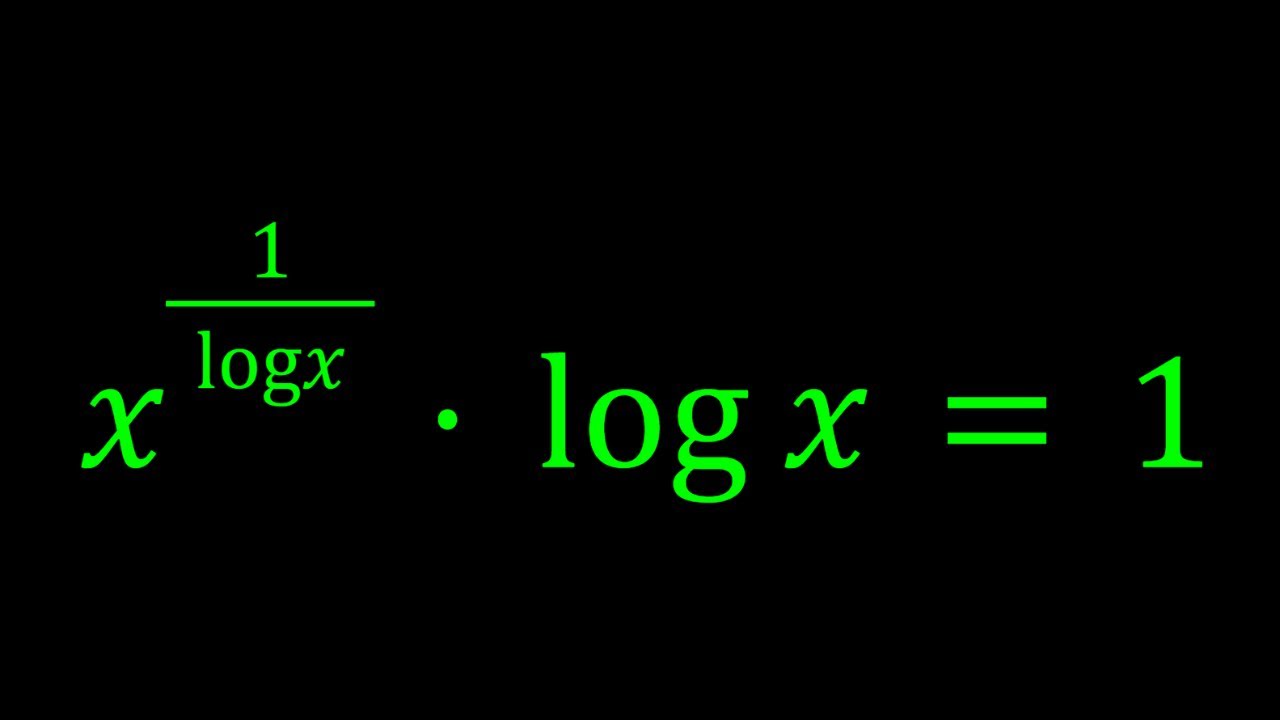
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #ExponentialEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
Solving Exponential and Logarithmic Equations
Solving Logarithmic Equations
How to Solve Exponential Equations using Logarithms - No Common Base Present
Solving Exponential Equations
Solving exponential equation with logarithm | Logarithms | Algebra II | Khan Academy
Solving Exponential and Logarithmic Equations (Multiple Examples)
Solving logarithmic equations | Exponential and logarithmic functions | Algebra II | Khan Academy
Introduction to Solving Logarithms and Exponentials (Precalculus - College Algebra 57)
Maths Logarithms#shorts #maths #logarithm #viralshort #genius #solution #ytshorts
Learn how to take log of both sides to solve an exponential equation
Lesson 3 Logarithms, Solving Logarithmic and Exponential Equations
Writing Logarithmic Equations In Exponential Form
Exponential Equation - Let’s solve the equation using logarithms
Logarithm Change of Base Formula & Solving Log Equations - Part 1 - [7]
Solving exponential equation | Exponential and logarithmic functions | Algebra II | Khan Academy
Solving an exponential equation with different bases
Solving exponential equations by using the natural log
Solving Logarithmic Equations... How? (NancyPi)
Solving exponential equations in terms of logs
Logarithms - The Easy Way!
Solving logarithmic equations by factoring
Logs Everything You Need to Know
How to Solve Exponential Equations using Logarithms: Step-by-Step Technique
How do I find x? Exponential equation with two different bases. Reddit precalculus r/Homworkhelp
Комментарии
 0:07:08
0:07:08
 0:25:27
0:25:27
 0:05:47
0:05:47
 0:16:36
0:16:36
 0:02:51
0:02:51
 0:12:27
0:12:27
 0:04:13
0:04:13
 0:34:46
0:34:46
 0:00:13
0:00:13
 0:02:57
0:02:57
 0:16:33
0:16:33
 0:03:07
0:03:07
 0:14:37
0:14:37
 0:23:32
0:23:32
 0:05:12
0:05:12
 0:03:01
0:03:01
 0:02:23
0:02:23
 0:15:05
0:15:05
 0:10:07
0:10:07
 0:10:20
0:10:20
 0:07:00
0:07:00
 0:20:27
0:20:27
 0:05:46
0:05:46
 0:07:47
0:07:47