filmov
tv
6 ÷ 2 (2 + 1) = CORRECT WAY TO SOLVE

Показать описание
This is how to do the equation: 6 / 2 (2 + 1) = x to get the right answer of 9. This is the correct way. I also show how people are getting the wrong answer of 1. Post this on facebook to end this dumb argument forever. I am tired of having to explain this to every person I meet.
If anyone has any questions or arguments, post them and I will respond to them. This is the correct way to solve the equation.
If anyone has any questions or arguments, post them and I will respond to them. This is the correct way to solve the equation.
6÷2(1+2) = ? Correct Answer Explained By Mathematician
6÷2(1+2)=???
Math Prof answers 6÷2(1+2) = ? once and for all ***Viral Math Problem***
6÷2(1+2) = ? Correct Answer Explained | Viral Math Problem | Viral Math Problem 6÷2(1+2)=
Deepa Yen Madtha Ideya || 6 5=2 || Final Clip 30
6÷2(1+2) = ? | Correct Answer Inside Finally Solved!! | PEMDAS/BIDMAS is Wrong?!
6^2 ÷ 2(3) + 4 = ? Mathematician Explains The Correct Answer
6/2(1+2) or 6÷2(1+2) equals ? The truth.
FK Sarajevo 2:2 HŠK Posušje | 6. kolo WWin Lige 2024/25
НУ-КА, ВСЕ ВМЕСТЕ! 6 СЕЗОН - 2 ВЫПУСК
6 - 1 x 0 + 2 ÷ 2 = ? Mathematician Explains The Correct Answer
Learning the 6-2 (with Subs) Offensive in Volleyball
✓ Одиозный дед и Hitman. 6:2(1+2)=1 | В интернете опять кто-то неправ #003 | Борис Трушин...
Clever gelöst - 6/2-Wegeventil
Meet the Math Facts Addition & Subtraction - 2+4=6
EM Quali Deutschland - Österreich - 6:2 - 2.9.2011 - Tore / Zusammenfassung (HD 720p)
STIHL AutoCut C 6-2: Anleitung
6-2! | Highlights Feyenoord - Ajax | Eredivisie 2018-2019
6.2.2 Самый легкий путь / 6.2.2 Easy path / Марвел Битва Чемпионов...
Real Madrid 2 x 6 Barcelona ● La Liga 08/09 Extended Goals & Highlights HD
Volleyball Rotations 6-2
Learn Number Counting 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 | Numbers By RV AppStudios
REAL MADRID 2-6 BARÇA | Match highlights 2008/09
6÷2(1+2) = ? Mathematician Explains The Correct Answer | Viral Twitter Problem Solved By Aman Sir
Комментарии
 0:05:33
0:05:33
 0:01:21
0:01:21
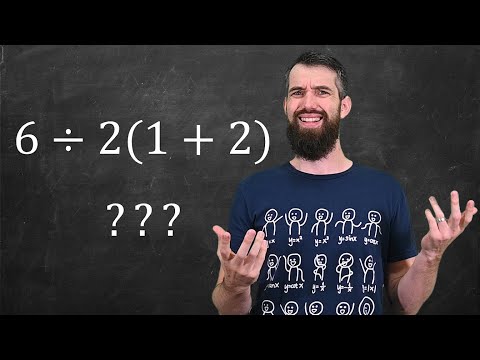 0:06:04
0:06:04
 0:00:42
0:00:42
 0:03:52
0:03:52
 0:11:14
0:11:14
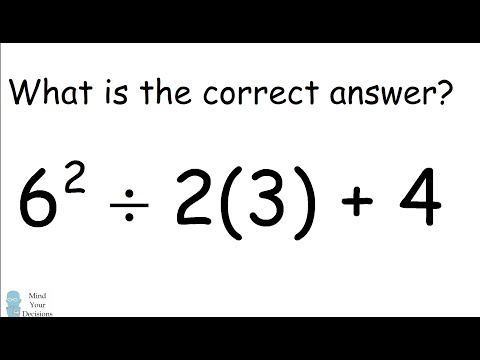 0:03:33
0:03:33
 0:10:20
0:10:20
 0:05:23
0:05:23
 2:09:59
2:09:59
 0:02:44
0:02:44
 0:04:06
0:04:06
 0:17:35
0:17:35
 0:00:29
0:00:29
 0:02:13
0:02:13
 0:11:00
0:11:00
 0:00:37
0:00:37
 0:14:07
0:14:07
 0:21:05
0:21:05
 0:14:57
0:14:57
 0:07:37
0:07:37
 0:12:30
0:12:30
 0:06:39
0:06:39
 0:09:02
0:09:02