filmov
tv
6/2 (1+2) had the world stumped but we finally have an answer! #shorts #maths #mathstricks

Показать описание
6/2 (1+2) had the world stumped but we finally have an answer! #shorts #maths #mathstricks
Math Prof answers 6÷2(1+2) = ? once and for all ***Viral Math Problem***
Viral Math Problem 6➗2(1+ 2)= ? Correct Answer Explained by mathematician!
The Problem with PEMDAS: Why Calculators Disagree
The Simplest Math Problem No One Can Solve - Collatz Conjecture
Learning Math
5 simple unsolvable equations
Approximating 2+2
Germany OUT! Belgium OUT! (World Cup 2022 Parody Cartoon Japan Spain)
AMAZING SQUID GAMES ALARM CLOCK ⏰🤯 #Shorts
6÷2(1+2) = ? Viral Math Puzzle Solved! | Mr.GK
9 TIMES TABLE #shorts #math #maths #mathematics
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Multiples of 8 😎 #Shorts #math #maths #mathematics
FULL FORM OF MATHS😍#maths #MATHSFUN#shorts #viral
One Two Buckle My Shoe by Edmondx & Blanco y Sancho #shorts
Kid sings One Two Buckle My Shoe on America's Got Talent
Table of 5 #mathsscam #tables #shorts #5
Overcooked 2 【World Record】Story 6-2 2 players Score 1330
Fractions Butterfly Method #Short Video #Maths
Meet the Math Facts Addition & Subtraction - 1+1=2
Numberblocks 1 to 100 | One Hundred Blocks Tall
6÷2(1+2) = ? Mathematician Explains The Correct Answer | Viral Twitter Problem Solved By Aman Sir
Indian vs Japanese Maths 🔥| Vedic Maths Trick for Fast Calculation | Speed Maths #trending #shorts...
Комментарии
 0:00:50
0:00:50
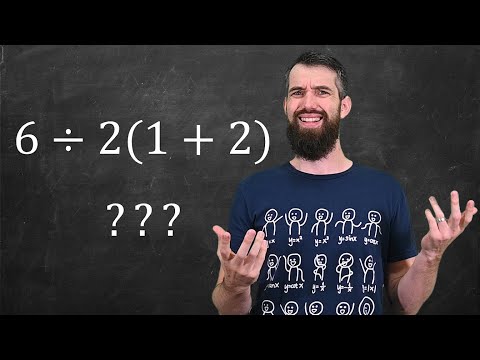 0:06:04
0:06:04
 0:06:18
0:06:18
 0:17:27
0:17:27
 0:22:09
0:22:09
 0:02:37
0:02:37
 0:00:50
0:00:50
 0:00:40
0:00:40
 0:02:32
0:02:32
 0:00:20
0:00:20
 0:10:38
0:10:38
 0:00:23
0:00:23
 0:00:52
0:00:52
 0:00:20
0:00:20
 0:00:41
0:00:41
 0:00:10
0:00:10
 0:00:37
0:00:37
 0:00:23
0:00:23
 0:03:48
0:03:48
 0:00:27
0:00:27
 0:02:13
0:02:13
 0:03:11
0:03:11
 0:09:02
0:09:02
 0:00:13
0:00:13