filmov
tv
A functional equation from Kyrgyzstan
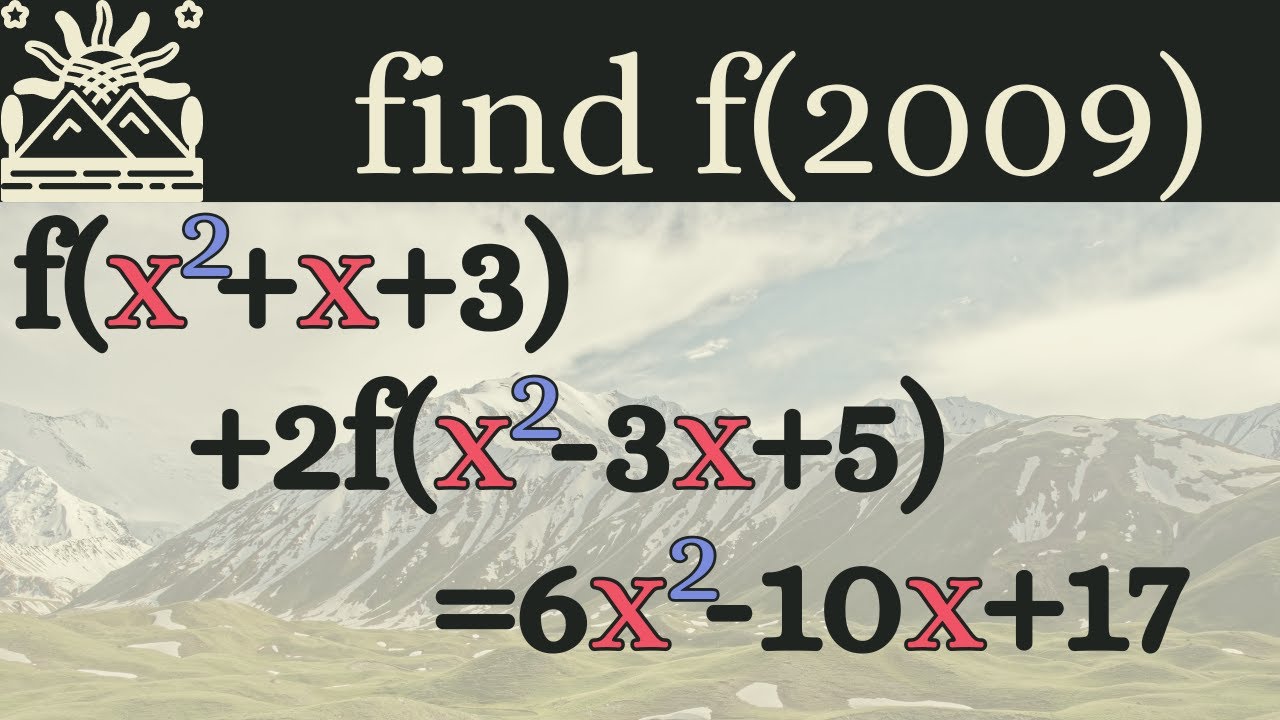
Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
A functional equation from Kyrgyzstan
17-July-2022 A functional equation from Kyrgyzstan 2009 (Michael Penn)
Kyrgyzstan Mathematical Olympiad 2012 | Two Ways to Solve This Functional Equation!
A functional equation from my favorite book.
One of the coolest functional equations I have seen!
a fun functional equation
A functional equation from @goodplacetostop2973
A functional equation from the Philippines.
Gaining Insights: Solving a Functional Equation
A functional equation from the Netherlands.
a nice functional equation.
A functional equation from Belgium | practice problems
Making a functional equation 'work'.
Destroying A Functional Equation Via Substitution
Thanks viewer for a nice functional equation!!
Finding f(25) from a Functional Equation || High School Math
A super nice Rational functional equation (Not real, or is it?😉)
An intriguing problem with my favorite function
Don't make eye contact
Israeli Army 🏅🪬 #bralcon
Can You Find An Easy Way to Solve the System of Equations?
A Beautiful trick for Functional Equations| Putnam 1988 A5
Involutions & Pointwise Trap | Kyrgyzstan National Math Olympiad 2012 | Problem 4 | Cheenta
Solving for f(2016) in the functional equation: f(x^2+x)+2f(x^2-3x+2)=9x^2-15x || High School Math
Комментарии
 0:12:02
0:12:02
 0:00:29
0:00:29
 0:10:15
0:10:15
 0:11:23
0:11:23
 0:15:34
0:15:34
 0:09:20
0:09:20
 0:08:18
0:08:18
 0:07:44
0:07:44
 0:10:22
0:10:22
 0:08:47
0:08:47
 0:18:42
0:18:42
 0:03:21
0:03:21
 0:10:04
0:10:04
 0:00:42
0:00:42
 0:07:16
0:07:16
 0:07:53
0:07:53
 0:19:33
0:19:33
 0:10:14
0:10:14
 0:00:05
0:00:05
 0:00:19
0:00:19
 0:06:28
0:06:28
 0:05:21
0:05:21
 0:19:53
0:19:53
 0:11:57
0:11:57