filmov
tv
Proof: ax+b is Continuous using Epsilon Delta Definition
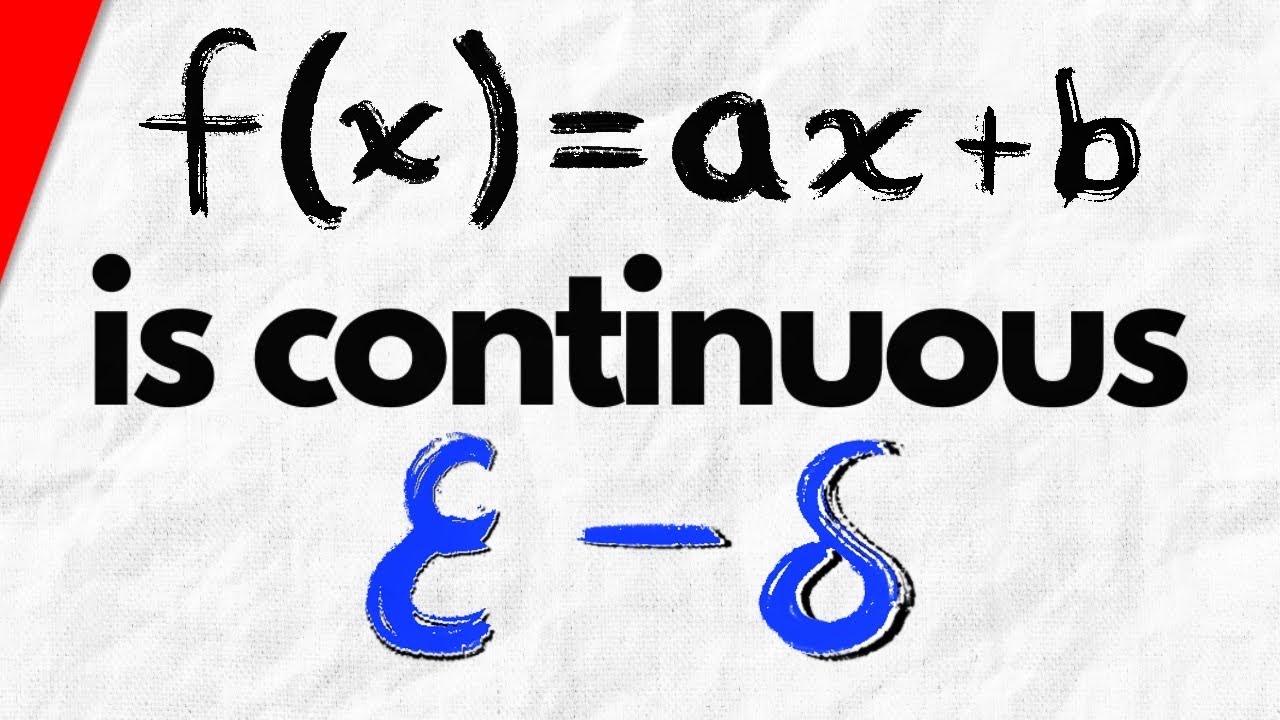
Показать описание
We prove that f(x)=mx+b, a general linear function, is continuous on its entire domain - the real numbers. We complete this proof using the epsilon delta definition of continuity of a function at a point. To do this, we simply take an epsilon greater than 0 and an arbitrary point c from our domain, then go through the motions of finding a delta greater than 0 so that any x in D that is within delta of c has an image within epsilon of c's image. In this case, it will be very easy, with one sidenote necessary for the m=0 case of a constant function. Let me know if there are more epsilon delta continuity proofs you want to see!
◉Textbooks I Like◉
★DONATE★
Thanks to Loke Tan, Matt Venia, Micheline, Doug Walker, Odd Hultberg, Marc, Roslyn Goddard, Shlome Ashkenazi, Barbora Sharrock, Mohamad Nossier, Rolf Waefler, Shadow Master, and James Mead for their generous support on Patreon!
Outro music is mine. You cannot find it anywhere, for now.
Follow Wrath of Math on...
◉Textbooks I Like◉
★DONATE★
Thanks to Loke Tan, Matt Venia, Micheline, Doug Walker, Odd Hultberg, Marc, Roslyn Goddard, Shlome Ashkenazi, Barbora Sharrock, Mohamad Nossier, Rolf Waefler, Shadow Master, and James Mead for their generous support on Patreon!
Outro music is mine. You cannot find it anywhere, for now.
Follow Wrath of Math on...
Proof: ax+b is Continuous using Epsilon Delta Definition
How REAL Men Integrate Functions
Population variance of aX+b
When mathematicians get bored (ep1)
NEWYES Calculator VS Casio calculator
##Var(ax) =a^2 var(x)##proof##Basic Probability#####Part-A question#####
4 2 AxB is not BxA
Properties of aX + b
OCR MEI Statistics Minor F: Discrete Random Variables: 09 E(aX+b)
IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit
Linear Algebra | S01E08 System of Equations, Ax=0 & Ax=b | B.A/M.A Economics Entrance ISI/DSE
Proof: sqrt(x) is Continuous using Epsilon Delta Definition | Real Analysis Exercises
Find the values a and b that make the piecewise function continuous
show that Var(aX+b) = a^2Var(X)
1st yr. Vs Final yr. MBBS student 🔥🤯#shorts #neet
Proof: f(x) = x is Continuous using Epsilon Delta Definition | Real Analysis Exercises
Before JEE vs After JEE 😍 | My Transformation💔 | IIT Motivation|Jee 2023 #transformation #iit #viral...
Cosplay by b.tech final year at IIT Kharagpur
If y = tan⁻¹(ax - b/bx + a) , Find dy/dx
2-2a Properties of aX+b
Lec-12: Prove that E(a)=a, E(ax)=aE(x) & E(ax+b)=aE(x)+b | Important proves
Aspirants practicing eatingetiquette # SSB #SSBPreparation #NDA #CDS #Defence #DefenceAcademy
Differentiate the function w.r.t.x sin(ax+b)|NCERT|12|Part 1|Continuity and Differentiability|Ex 5.2
Maths Ki Problem 😜 PIHOOZZ
Комментарии
 0:03:40
0:03:40
 0:00:35
0:00:35
 0:03:44
0:03:44
 0:00:37
0:00:37
 0:00:14
0:00:14
 0:01:24
0:01:24
 0:01:02
0:01:02
 0:05:53
0:05:53
 0:02:26
0:02:26
 0:00:12
0:00:12
 0:09:47
0:09:47
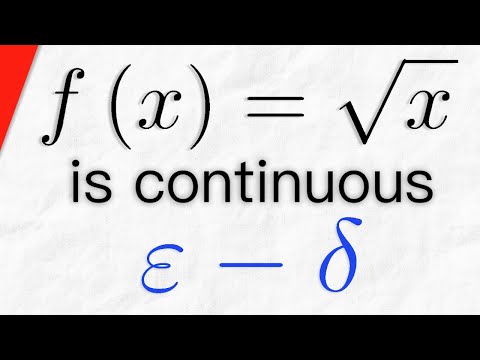 0:09:22
0:09:22
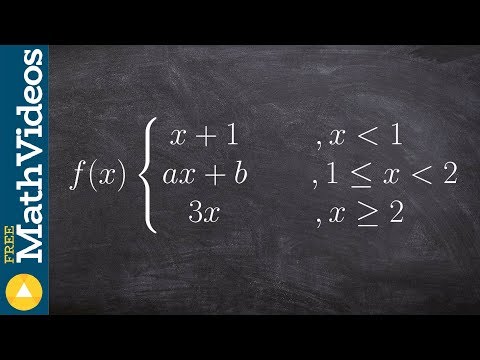 0:03:44
0:03:44
 0:35:14
0:35:14
 0:00:20
0:00:20
 0:04:46
0:04:46
 0:00:20
0:00:20
 0:00:15
0:00:15
 0:06:06
0:06:06
 0:06:39
0:06:39
 0:08:58
0:08:58
 0:00:11
0:00:11
 0:01:49
0:01:49
 0:00:23
0:00:23