filmov
tv
A System of Equations with Integer Solutions
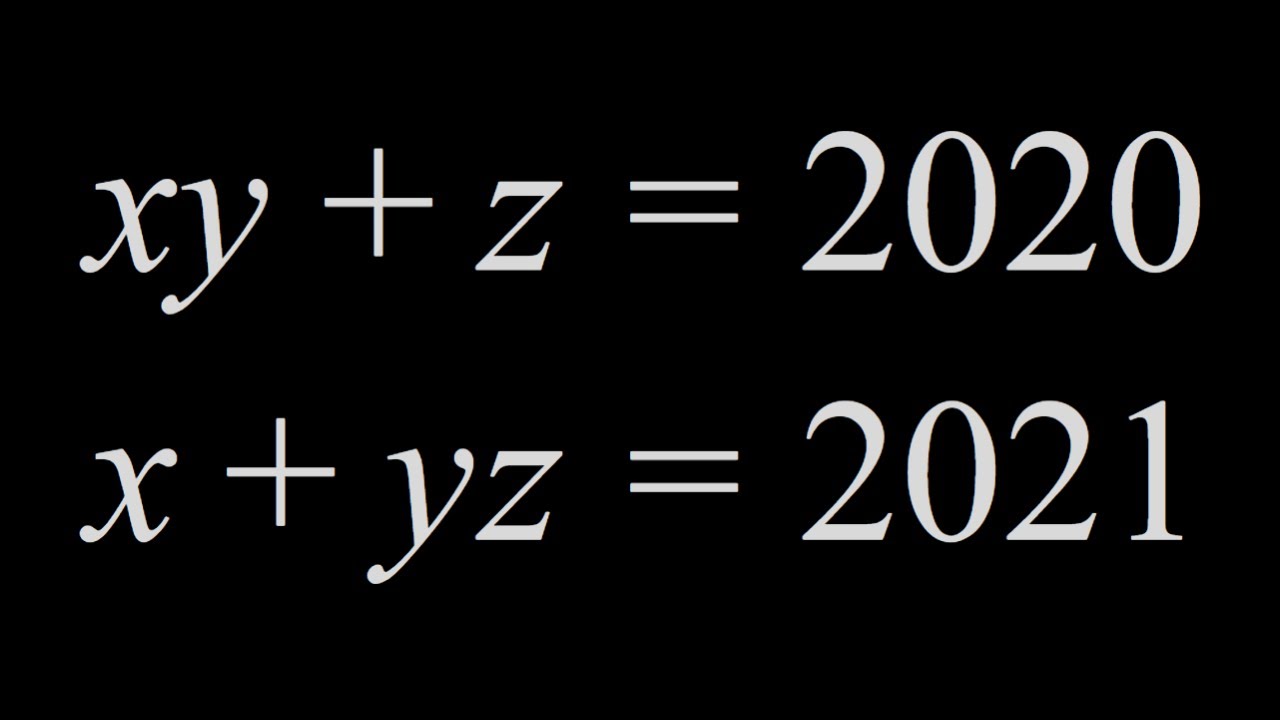
Показать описание
If you need to post a picture of your solution or idea:
#NumberTheoryProblems #DiophantineSystems
EXPLORE 😎:
PLAYLISTS 🎵 :
#NumberTheoryProblems #DiophantineSystems
EXPLORE 😎:
PLAYLISTS 🎵 :
Solving Systems of Equations By Elimination & Substitution With 2 Variables
Solving Systems of Equations With 3 Variables & Word Problems
How do we solve a system of linear equations using any method
Solving Systems of Equations By Graphing
Linear Algebra - 27 - Algebraic Systems of Equations with Matrices
Learn to solve a system of equations using substitution
Substitution Method to Solve a System of Equations
Solving systems of equations by elimination | Algebra Basics | Khan Academy
Grade 10 - Math: Systems of linear equations 2
Elimination Method For Solving Systems of Linear Equations Using Addition and Multiplication, Algebr
One Solution, No Solution, or Infinitely Many Solutions - Consistent & Inconsistent Systems
Solve a system of linear equations using substitution
Solving Systems of Equations... Elimination Method (NancyPi)
Solving a system of equations by substitution
SOLVING SYSTEMS OF EQUATIONS STEP-BY-STEP!
Solving Systems of Equations... Substitution Method (NancyPi)
Solving a System of Equations Using Elimination and Multipliers
Systems of Quadratic Equations
Linear Algebra - Solving Systems of Equations
[October SAT Math] Systems Of Equations - TRICKS & SHORTCUTS + Matching Rule (Score Higher)
13 - Overview of Systems of Linear Equations (Simultaneous Equations & Systems of Equations)
Solving System of Linear Equations by Substitution Method | Solution of System of Equations
Learn the Basics for Solving a System of Equations by Elimination
Solve a system of three variables
Комментарии
 0:10:27
0:10:27
 0:12:44
0:12:44
 0:04:34
0:04:34
 0:05:15
0:05:15
 0:07:18
0:07:18
 0:05:17
0:05:17
 0:03:47
0:03:47
 0:12:44
0:12:44
 0:42:52
0:42:52
 0:10:21
0:10:21
 0:07:30
0:07:30
 0:05:03
0:05:03
 0:19:44
0:19:44
 0:02:54
0:02:54
 0:04:49
0:04:49
 0:18:30
0:18:30
 0:03:48
0:03:48
 0:11:20
0:11:20
 0:05:59
0:05:59
![[October SAT Math]](https://i.ytimg.com/vi/yYeIFsby4tQ/hqdefault.jpg) 0:15:06
0:15:06
 0:28:36
0:28:36
 0:12:28
0:12:28
 0:07:10
0:07:10
 0:12:45
0:12:45