filmov
tv
Proof of (-1) (-1) = 1
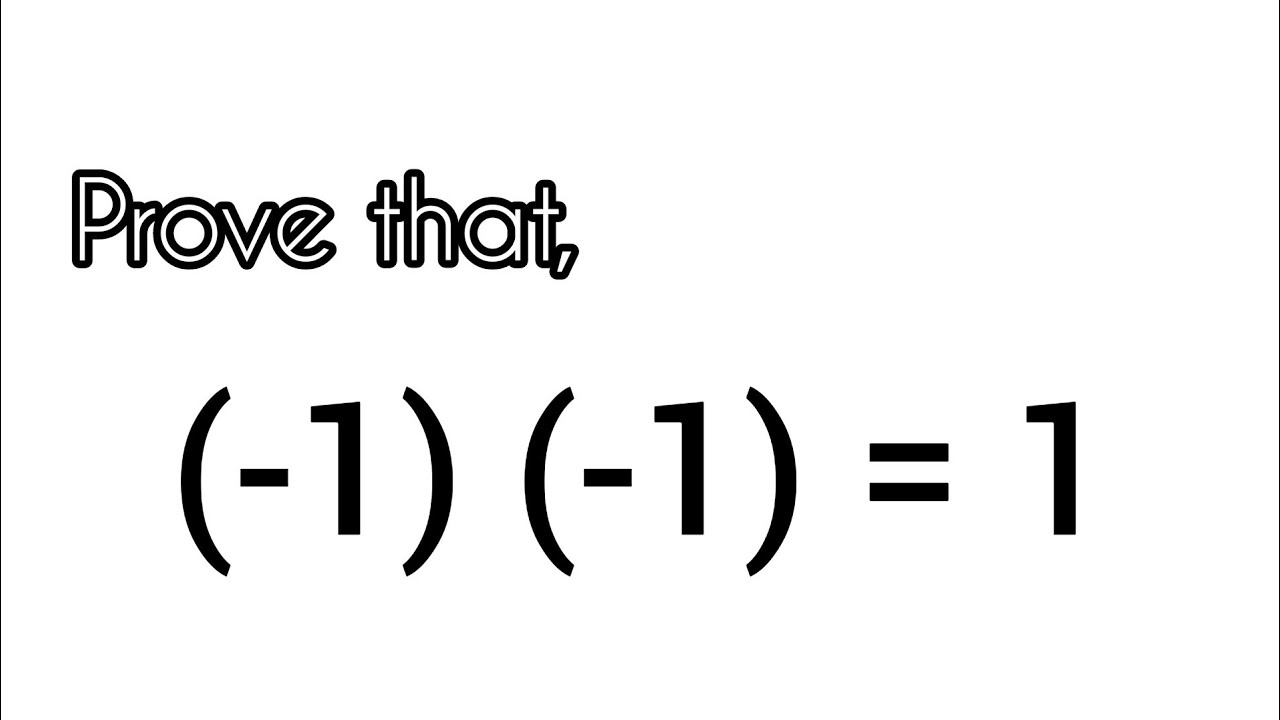
Показать описание
We all know that (-1)(-1) = 1. But do we know how to prove this simple mathematical statement that we take for granted. In this video I tried to explain the proof!
If you need a online private tutor you can contact with my friend Thil. He can teach you Math and Science. This is his facebook page:
#maths #mathematics #number #mathematical #mathematicalproofs #numbertheory #deductivereasoning #axiom #algebra #abstractalgebra #linearalgebra #realnumbers
If you need a online private tutor you can contact with my friend Thil. He can teach you Math and Science. This is his facebook page:
#maths #mathematics #number #mathematical #mathematicalproofs #numbertheory #deductivereasoning #axiom #algebra #abstractalgebra #linearalgebra #realnumbers
The 360-Page Proof That 1+1=2
The 379 page proof that 1+1=2
Actual Proof 1+1=2
Proof that 1+1 = 2 【Fundamentals of Mathematics】
1+1=3 Proof! #trick #shorts
I'm Settling This Math Debate Forever (.99 repeating = 1)
1 + 1 = 3 Proof | Breaking the rules of mathematics
0.999999… = 1
(ASMR) PROOF that 1 = 2 #Shorts
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
0.9 Repeating Equal to 1 Algebraic Proof | Fun Math JusticeTheTutor #shorts #maths #math
Proof 1+1=1 || Prove that 1+1=1 || How to prove 1+1=1 || Funny math proof
Proof that 1 = 2.
Every PROOF you've seen that .999... = 1 is WRONG
Approximating 2+2
Proof #1: Does 1 = 2?
Math's Fundamental Flaw
1=2 Proof
proof that 1=2 by a professor
why 0!=1 in 30 Seconds. (Shortest 0 factorial proof) #shorts
Proof by induction | Sequences, series and induction | Precalculus | Khan Academy
1= -1 False Proof Meme #short
Proof: Supremum of {n/(n+1)} = 1 | Real Analysis
THE EASIEST PROOF OF 1=0 IN 15 SECONDS!
Комментарии
 0:06:03
0:06:03
 0:16:43
0:16:43
 0:03:02
0:03:02
 0:12:16
0:12:16
 0:00:23
0:00:23
 0:04:11
0:04:11
 0:08:25
0:08:25
 0:01:00
0:01:00
 0:00:59
0:00:59
 0:00:38
0:00:38
 0:01:01
0:01:01
 0:02:17
0:02:17
 0:02:59
0:02:59
 0:09:25
0:09:25
 0:00:40
0:00:40
 0:01:00
0:01:00
 0:34:00
0:34:00
 0:00:58
0:00:58
 0:01:31
0:01:31
 0:00:30
0:00:30
 0:09:23
0:09:23
 0:00:28
0:00:28
 0:10:20
0:10:20
 0:00:36
0:00:36