filmov
tv
The 379 page proof that 1+1=2

Показать описание
Hi! I'm Jade. If you'd like to consider supporting Up and Atom, head over to my Patreon page :)
Visit the Up and Atom store
Subscribe to Up and Atom for physics, math and computer science videos
Principia Mathematica
Russell's Paradox video:
0:00 Intro
0:52 All was well in the land of math
1:39 Oh no! Trouble is brewing
3:47 The heroes of the story
5:06 Principia Mathematica
5:49 Logic
7:42 Formal Systems
9:52 Struggles :(
11:49 Ideas in 1+1=2
14:26 Failure
15:04 Sponsor
*Follow me* @upndatom
*A big thank you to my AMAZING PATRONS!*
Creator - Jade Tan-Holmes
Animations - Tom Groenestyn
Music - epidemic sound
The 379 page proof that 1+1=2
1 + 1 = 2: The Proof That Took 379 Pages! 🧐
The 360-Page Proof That 1+1=2
A visual infinite sum like you’ve never seen!
0.999999… = 1
1=2 Proof
270-year-old math problem SOLVED! Grazing goat problem
Breaking the rules of math
Proof of 1=-1 | What's wrong? #shorts
Math proof by picture #shorts
Proof that 1 + 1 = 3 [ Fundamentals of Mathematics ] #shorts
Geometry of sums of powers of 1/5
This Result Keeps Me Up At Night
Multiples of 8 😎 #Shorts #math #maths #mathematics
The Ending of One Piece...😥
Proof that 2+2 = 4
Mh370 Found 😱In✈️Google Map|Malaysia Airlines Flight 370 Founded|Google Map Secrets|
How To Figure Out Math Proofs On Your Own
#248 proof Godzilla is real . Godzilla in google earth #shorts
Only U.S. President to prove a theorem
3 Signs Your Manifestations are Coming Your Way
Proof #1: Does 1 = 2?
Safety shoe quality testing 0213+0213YW-1.#safetyshoes #workshoes #shoes#workboots
Isaac Newton The Principia #shorts
Комментарии
 0:16:43
0:16:43
 0:03:15
0:03:15
 0:06:03
0:06:03
 0:00:57
0:00:57
 0:01:00
0:01:00
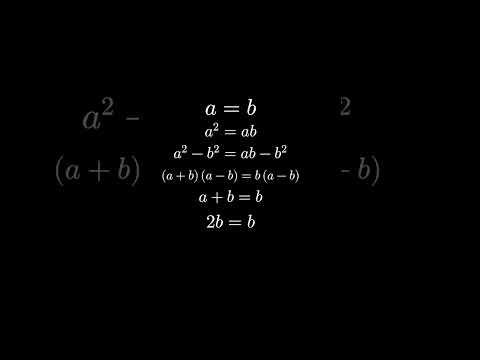 0:00:58
0:00:58
 0:01:00
0:01:00
 0:01:00
0:01:00
 0:00:23
0:00:23
 0:00:26
0:00:26
 0:00:36
0:00:36
 0:00:53
0:00:53
 0:08:53
0:08:53
 0:00:20
0:00:20
 0:00:09
0:00:09
 0:00:04
0:00:04
 0:00:38
0:00:38
 0:09:00
0:09:00
 0:00:41
0:00:41
 0:01:00
0:01:00
 0:00:40
0:00:40
 0:01:00
0:01:00
 0:00:26
0:00:26
 0:00:15
0:00:15