filmov
tv
Actual Proof 1+1=2

Показать описание
Become a Math Master With My Intro To Proofs Course! (FREE ON YOUTUBE)
This video presents a clear and concise proof of why 1+1 equals 2, a fundamental concept in mathematics. It breaks down the logic and reasoning behind this basic equation, making it understandable for anyone interested in math.
🙏Support me by becoming a channel member!
#math #brithemathguy #mathematics
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information. Viewers should always verify the information provided in this video by consulting other reliable sources.
This video presents a clear and concise proof of why 1+1 equals 2, a fundamental concept in mathematics. It breaks down the logic and reasoning behind this basic equation, making it understandable for anyone interested in math.
🙏Support me by becoming a channel member!
#math #brithemathguy #mathematics
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information. Viewers should always verify the information provided in this video by consulting other reliable sources.
Actual Proof 1+1=2
The 360-Page Proof That 1+1=2
Proof that 1+1 = 2 【Fundamentals of Mathematics】
How to prove 1+1=2 (seriously)
The 379 page proof that 1+1=2
Proof of 1-1=2
1=2 Proof
1 + 1 = 3 Proof | Breaking the rules of mathematics
LAST DAY GLOBAL RANK 677.BASE LINK PROOF ANTI 3 STAR TH17 BASE LINK | TH17 WAR BASE LINK 2024
Proving that 1/1 + 1/2 + 1/3 + 1/4... approaches INFINITY! #shorts
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Something Strange Happens When You Keep Squaring
Proof that 1 = 2.
proof that 1=2 by a professor
Proving God exists using Math
Approximating 2+2
(ASMR) PROOF that 1 = 2 #Shorts
Human Calculator Solves World’s Longest Math Problem #shorts
0.999999… = 1
Every Student Should See This
6÷2(1+2)=???
Proof #1: Does 1 = 2?
1+1=3 Proof! #trick #shorts
When mathematicians get bored (ep1)
Комментарии
 0:03:02
0:03:02
 0:06:03
0:06:03
 0:12:16
0:12:16
 0:03:39
0:03:39
 0:16:43
0:16:43
 0:00:09
0:00:09
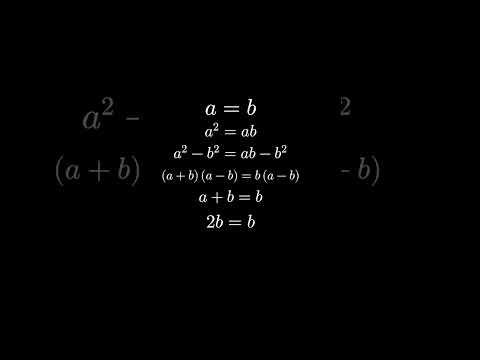 0:00:58
0:00:58
 0:08:25
0:08:25
 0:02:48
0:02:48
 0:00:54
0:00:54
 0:00:38
0:00:38
 0:33:06
0:33:06
 0:02:59
0:02:59
 0:01:31
0:01:31
 0:05:23
0:05:23
 0:00:40
0:00:40
 0:00:59
0:00:59
 0:00:34
0:00:34
 0:01:00
0:01:00
 0:00:58
0:00:58
 0:01:21
0:01:21
 0:01:00
0:01:00
 0:00:23
0:00:23
 0:00:37
0:00:37