filmov
tv
0.9 Repeating Equal to 1 Algebraic Proof | Fun Math JusticeTheTutor #shorts #maths #math

Показать описание
I'm Settling This Math Debate Forever (.99 repeating = 1)
0.9 Repeating Equal to 1 Algebraic Proof | Fun Math JusticeTheTutor #shorts #maths #math
Does 0.999... = 1?
Every PROOF you've seen that .999... = 1 is WRONG
0.999... Repeating Is Equal To 1, But Something Like It Is Not (Introduction To The Surreal Numbers)
0.9 repeating
Why is 0.9 repeating equal to 1? What it really means…
Exploring .9 repeating
9th Maths | Chapter 2 - Important 2 Mark Questions | Public Exam 2025 | Janasruthi Ma'am
.9 Repeating is Equal to One
Does 0.9999 repeating equal 1?
Does .9 repeating equal 1?
GOOD Proof that 0.9 Repeating Equals 1
The One about 0.999… Repeating Equals 1 // Math Minute [#42] [ALGEBRA] [NUMBER THEORY]
Read video description: Explaining the equality between 1 and 0.9... [9's repeating]
0.9 Repeating Equal to 1 Algebraic Proof | Fun Math #shorts #maths #mathstricks #priyanka_prajapati
GOOD Proof that 0.9 Repeating Equals 1, the Good Version
Does .9 repeating equal 1?
Repeating Decimal Fun
998,001 and its Mysterious Recurring Decimals - Numberphile
Simple Proof That 0.99 Repeating Is Equal To 1:
Pure Repeating Decimal to Fractions - How to Convert
Fun Math | 0.9 Repeating Equal to 1 Algebraic Proof #shorts #maths #math
Does 0.9 repeating equal 1?
Комментарии
 0:04:11
0:04:11
 0:01:01
0:01:01
 0:02:27
0:02:27
 0:09:25
0:09:25
 0:08:08
0:08:08
 0:01:00
0:01:00
 0:06:23
0:06:23
 0:02:06
0:02:06
 0:34:12
0:34:12
 0:04:20
0:04:20
 0:08:52
0:08:52
 0:04:14
0:04:14
 0:02:01
0:02:01
 0:09:26
0:09:26
 0:00:53
0:00:53
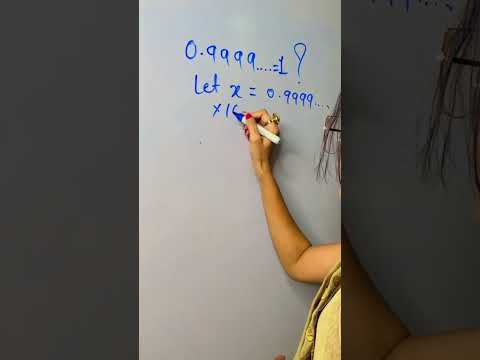 0:00:18
0:00:18
 0:09:31
0:09:31
 0:02:19
0:02:19
 0:02:02
0:02:02
 0:09:47
0:09:47
 0:01:00
0:01:00
 0:00:49
0:00:49
 0:01:00
0:01:00
 0:02:21
0:02:21