filmov
tv
Abstract Algebra | The kernel of a homomorphism

Показать описание
We give the definition of the kernel of a homomorphism, prove some of its properties, and give some examples.
The Kernel of a Group Homomorphism – Abstract Algebra
Kernels of Homomorphisms | Abstract Algebra
Abstract Algebra | The kernel of a homomorphism
Abstract Algebra 10.4: Homomorphisms and Kernels
Abstract Algebra Homomorphisms Kernel is a Subgroup
Image and Kernel
kernel of group homomorphism Example 1
Abstract Algebra 1.3: The Kernel And Subgroups
Kernel and Image of Homomorphism #set #topology #functions #maths #love #abstract #algebra #groups
Abstract Algebra Homomorphisms One to One Trivial Kernel
Definition of the Kernel of a Group Homomorphism and Sample Proof
A Kernel Theorem: f(a)=f(b) iff Ka=Kb | Abstract Algebra
Kernel of Homomorphism | Group Theory - 28 | Abstract Algebra | Mathematics | Academic Lectures
Kernel of a group homomorphism
Abstract Algebra: The Kernel of a Homomorphism is a Normal Subgroup (Fundamental Theorem part 1)
Abstract Algebra 1.4 : Kernels and Normal Subgroups
Kernel (algebra)
Kernel of a Homomorphism is a Normal Subgroup of G | Abstract Algebra Exercises
Kernel of homomorphism||Theorems||Group theory||Abstract algebra||Lecture 14
Ring Homomorphism, Kernel of Homomorphism and Ideals [Abstract Algebra]
Abstract Algebra - 10.1 Group Homomorphisms and Properties
Abstract Algebra: kernel injectivity Thm, subgroup lattice, review, 9-17-18
Abstract Alg, Lec 21A: Internal Direct Products, Homomorphisms, Kernels, First Isomorphism Theorem
Proof: Basic Properties of Homomorphisms (Identities and Inverses) | Abstract Algebra
Комментарии
 0:04:53
0:04:53
 0:11:04
0:11:04
 0:10:01
0:10:01
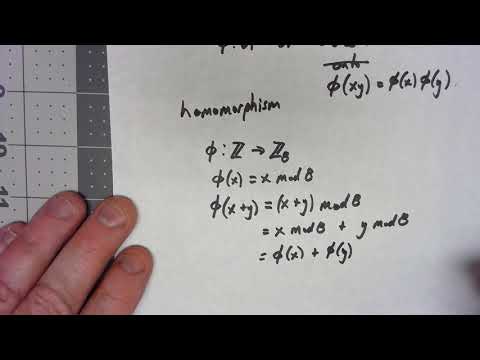 0:07:50
0:07:50
 0:01:29
0:01:29
 0:05:35
0:05:35
 0:06:27
0:06:27
 0:11:51
0:11:51
 0:12:35
0:12:35
 0:02:17
0:02:17
 0:09:00
0:09:00
 0:05:14
0:05:14
 0:13:19
0:13:19
 0:06:31
0:06:31
 0:25:44
0:25:44
 0:11:34
0:11:34
 0:11:50
0:11:50
 0:04:25
0:04:25
 0:24:27
0:24:27
 0:15:26
0:15:26
 0:18:03
0:18:03
 0:49:11
0:49:11
 0:36:50
0:36:50
 0:05:57
0:05:57