Abstract Algebra: The Kernel of a Homomorphism is a Normal Subgroup (Fundamental Theorem part 1)

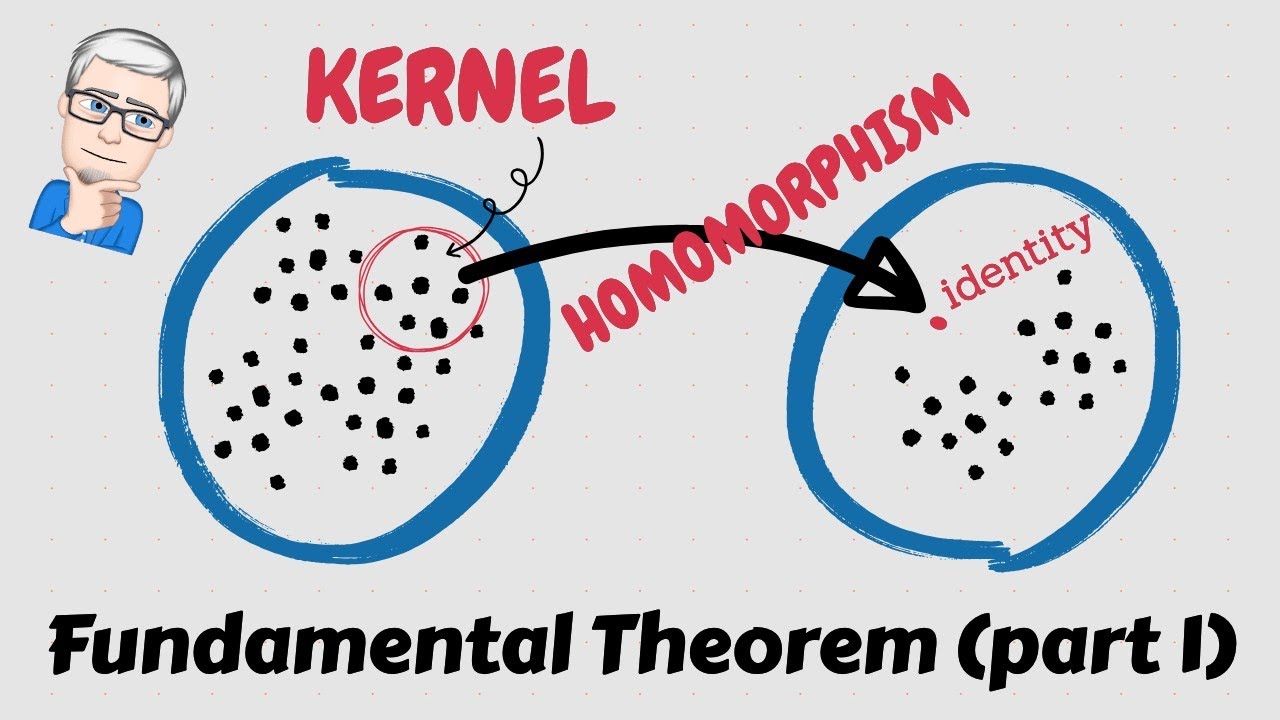
If h is a homomorphism from a group G1 to a group G2, then the set of elements of G1 that get sent to the identity element of G2 turns out to form a subgroup of G1. Moreover, this distinguished subgroup turns out to be normal in G1. We call this subgroup K and refer to it as the "vanishing set" of h. (The standard terminology is the "kernel" of h, but the vanishing set of a homomorphism is more descriptive than the kernel of a homomorphism.) Because K is normal in G1, the collection of cosets of K forms a group called the quotient group (alternatively, factor group) of G1 with respect to K, and is denoted as G1/K. The fundamental theorem of group homomorphisms says that G1/K is algebraically identical to a subgroup of G2. In fact, G1/K is isomorphic to G2 if h is a surjective function.

This video shows that the vanishing set of a homomorphism, i.e., the kernel of a homomorphism is a normal subgroup. This is part 1 of the Fundamental Theorem of Group Homomorphisms which is the most important result in the study of Group Theory.