filmov
tv
Kernels of Homomorphisms | Abstract Algebra

Показать описание
We introduce kernels of homomorphisms. We give the definition of kernel in group theory, an example of a kernel of a homomorphism onto the additive group of real numbers, then finish by proving the kernel of a homomorphism is a normal subgroup of the domain group of the homomorphism. #abstractalgebra #grouptheory
Fundamental Homomorphism Theorem: (coming soon)
0:00 - Intro
0:33 - Definition of Kernel of a Homomorphism
1:26 - Example of a Kernel of a Homomorphism
5:08 - Proof Kernel is a Normal Subgroup
10:21 - Outro
◉Textbooks I Like◉
★DONATE★
Thanks to Petar, dric, Rolf Waefler, Robert Rennie, Barbara Sharrock, Joshua Gray, Karl Kristiansen, Katy, Mohamad Nossier, and Shadow Master for their generous support on Patreon!
Follow Wrath of Math on...
Fundamental Homomorphism Theorem: (coming soon)
0:00 - Intro
0:33 - Definition of Kernel of a Homomorphism
1:26 - Example of a Kernel of a Homomorphism
5:08 - Proof Kernel is a Normal Subgroup
10:21 - Outro
◉Textbooks I Like◉
★DONATE★
Thanks to Petar, dric, Rolf Waefler, Robert Rennie, Barbara Sharrock, Joshua Gray, Karl Kristiansen, Katy, Mohamad Nossier, and Shadow Master for their generous support on Patreon!
Follow Wrath of Math on...
Kernels of Homomorphisms | Abstract Algebra
The Kernel of a Group Homomorphism – Abstract Algebra
Abstract Algebra | The kernel of a homomorphism
Abstract Algebra 10.4: Homomorphisms and Kernels
Abstract Algebra 58: Kernels of homomorphisms
Abstract Algebra Homomorphisms Kernel is a Subgroup
Abstract Algebra Homomorphisms Kernels are Normal
Kernel of a group homomorphism
Intro to Group Homomorphisms | Abstract Algebra
Homomorphisms (Abstract Algebra)
Definition of the Kernel of a Group Homomorphism and Sample Proof
Abstract Algebra Homomorphisms One to One Trivial Kernel
Abstract Algebra - 10.1 Group Homomorphisms and Properties
Abstract Algebra | Ring homomorphisms
Abstract Algebra Homomorphisms Examples
Abstract Algebra Ring Homomorphisms Kernels
Abstract Algebra Homomorphisms Examples
Abstract Algebra. Homomorphisms 2
Abstract Algebra: Exam 2 Review (Group Homomorphisms, Kernels, Preimages, Factor Groups)
Kernels of Ring Homomorphisms
Kernel of a Group Homomorphism is a Normal Subgroup Proof
Abstract Alg, Lec 21A: Internal Direct Products, Homomorphisms, Kernels, First Isomorphism Theorem
27 Kernels and one to one ring homomorphisms
Abstract Algebra Homomorphisms Inverse Images are Cosets
Комментарии
 0:11:04
0:11:04
 0:04:53
0:04:53
 0:10:01
0:10:01
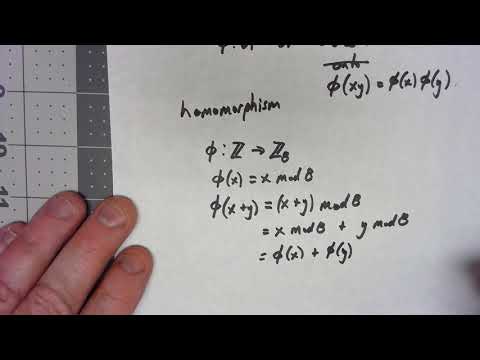 0:07:50
0:07:50
 0:09:56
0:09:56
 0:01:29
0:01:29
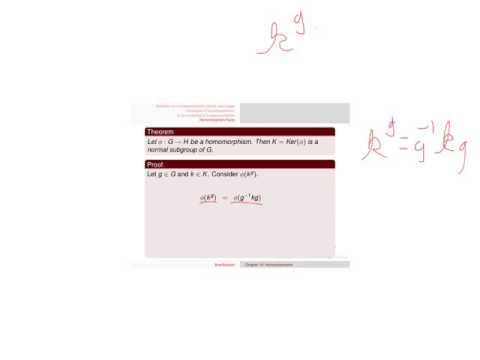 0:02:03
0:02:03
 0:06:31
0:06:31
 0:15:01
0:15:01
 0:04:12
0:04:12
 0:09:00
0:09:00
 0:02:17
0:02:17
 0:18:03
0:18:03
 0:20:01
0:20:01
 0:08:14
0:08:14
 0:10:14
0:10:14
 0:08:14
0:08:14
 0:22:39
0:22:39
 0:58:58
0:58:58
 0:14:31
0:14:31
 0:02:48
0:02:48
 0:36:50
0:36:50
 0:10:34
0:10:34
 0:02:17
0:02:17