Abstract Algebra 10.4: Homomorphisms and Kernels

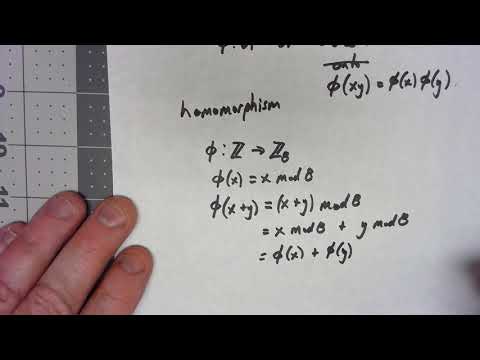
Homomorphisms are functions between groups that preserve the group operations. We consider this definition, look at some examples, and also look at a special subgroup based on the homomorphisms.

[tee.]

How is this so easy to understand when u say it, retook my uni exam 2 times now watched your video & it finally makes so much sense you need to train lecturers honestly! So good

[TheTessatje]

Great examples. Especially φ(x)=x^2 4:39, because it's also not one-to-one!

[hyperduality]

Before (a priori, group) is dual to after (a posteriori, image) -- Immanuel Kant.
Normal subgroups are dual to homomorphism (factor groups) synthesize the kernel.
Thesis is dual to anti-thesis creates the converging thesis or synthesis -- the time independent Hegelian dialectic.
Being is dual to non-being creates becoming -- Plato.
Domains (groups) are dual to codomains (image, range).
Points are dual to lines -- the principle of duality in geometry.
Null homotopic implies contraction to a point, non null homotopic requires at least two points (duality) -- topology.
Polar opposites of the dyad unite into one or the monad - opposame.
"Always two there are" -- Yoda.

[George]

For the final example, the ker(phi) = {1}, since it's from R*; -1 isn't in the domain.. right?

[Amitkumar-lsiu]

please do the same for z5 to z6 in another video