filmov
tv
Can you prove this inequality? | Moscow Mathematical Olympiad Problem

Показать описание
Given 𝒂, 𝒃 ∈ℝ^+, 𝒂 +𝒃 =𝟏, prove (𝒂+𝟏/𝒂)^𝟐 +(𝒃+𝟏/𝒃)^𝟐 ≥ 𝟐𝟓/𝟐. How to prove this inequality? We apply the GM-AM inequality to solve this problem.
Can you prove this Inequality?
Can you prove this inequality? | USSR Olympiad Problem | Prove 𝒏! ≤ ((𝒏+𝟏)/𝟐)^𝒏
Can you prove this CRAZY easy inequality?!
A Simple Way to Prove This Inequality | Olympiad Math
Turkey National Contests Question. Can you prove this inequality?
Belarus National Contests | Can you prove this inequality?
Moscow Middle School Math Olympiad Question. Can you prove this inequality in one minute?
Can You Prove the Inequality ???
Mid-Week Bible Experience: 'Navigating The Power Of A Storm-Proof Faith'
Can you prove this inequality? | Moscow Mathematical Olympiad Problem
St. Petersburg City Math Olympiad Question. Can You Prove this Inequality?
Can you prove this sequence inequality?
Inequality Mathematical Induction Proof: 2^n greater than n^2
Can You Prove the Triangle Inequality?
Proving a quick easy inequality #shorts
Czech and Slovak regional contests question. Can you prove the inequality?
Can you prove this inequality?
Can You Prove Bernoulli's Inequality?
AM-GM Inequality via negative space
Visual Cauchy-Schwarz Inequality
AM-GM inequality visually
Mean Inequalities
Triangle Inequality for Real Numbers Proof
Introduction to Inequality Proofs
Комментарии
 0:08:02
0:08:02
 0:02:40
0:02:40
 0:03:06
0:03:06
 0:06:20
0:06:20
 0:07:09
0:07:09
 0:05:31
0:05:31
 0:04:14
0:04:14
 0:03:23
0:03:23
 1:31:55
1:31:55
 0:05:56
0:05:56
 0:04:36
0:04:36
 0:07:56
0:07:56
 0:09:20
0:09:20
 0:03:01
0:03:01
 0:00:32
0:00:32
 0:06:37
0:06:37
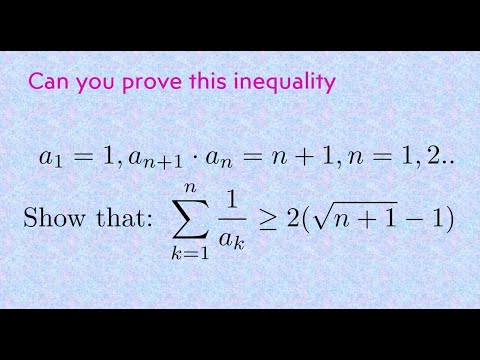 0:04:07
0:04:07
 0:03:03
0:03:03
 0:01:00
0:01:00
 0:01:01
0:01:01
 0:01:00
0:01:00
 0:01:00
0:01:00
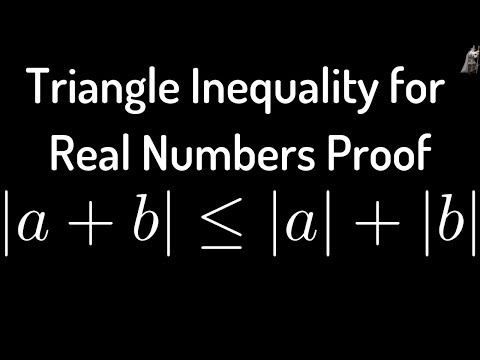 0:03:08
0:03:08
 0:12:05
0:12:05