filmov
tv
AM-GM Inequality via negative space

Показать описание
This is a short, animated visual proof demonstrating the arithmetic mean geometric mean inequality using algebraic areas and the Side-Angle-Side formula for a parallelogram.
For other visual proofs of this fact see:
For a nearly identical visual proof of another inequality (Cauchy-Schwarz) see
This animation is based on a visual proof that appears in Icons of Mathematics by Claudi Alsina and Roger B. Nelsen (MAA, 2011):
#mathshorts #mathvideo #math #amgminequality #mtbos #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #calculus #inequality
To learn more about animating with manim, check out:
For other visual proofs of this fact see:
For a nearly identical visual proof of another inequality (Cauchy-Schwarz) see
This animation is based on a visual proof that appears in Icons of Mathematics by Claudi Alsina and Roger B. Nelsen (MAA, 2011):
#mathshorts #mathvideo #math #amgminequality #mtbos #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #calculus #inequality
To learn more about animating with manim, check out:
AM-GM Inequality via negative space
Proof of the AM-GM Inequality
An elegant proof of AM - GM Inequality - Part 1
AM - GM INEQUALITY GEOMETRIC PROOF
An Application of AM-GM Inequality
the power mean
QM-AM-GM-HM inequality explained and shown
AM/GM Inequality (1 of 2: Geometric Proof)
AM-GM Inequality | Arithmetic Mean Geometric Mean Inequality
No Calculus, just AM-GM inequality.
AM-GM Geometric Proof In Under Three Minutes!
A Visual Proof of the Arithmetic Geometric Mean Inequality
09 - AM GM inequality for two variables
Trivial Inequality Introductory Problems and Video Solutions
AM-GM and Muirhead's Inequality
Nesbitt's inequality proof
The AM-GM Inequality - Introduction
AM-GM Inequality and Lagrange Multipliers
Arithmetic-Geometric Mean Inequality
JEE Delight | 4 vital inequalities | AM GM HM | Weighted mean | Mth power | Power mean inequality
How much does a PHYSICS RESEARCHER make?
Real Analysis, Lecture 4 (Arithmetic and Geometric Means Inequality and ±∞)
AM - GM Inequality (Part 2) | Problems
Some problems in AM GM inequality
Комментарии
 0:01:00
0:01:00
 0:12:04
0:12:04
 0:06:48
0:06:48
 0:00:58
0:00:58
 0:00:54
0:00:54
 0:00:47
0:00:47
 0:21:15
0:21:15
 0:13:12
0:13:12
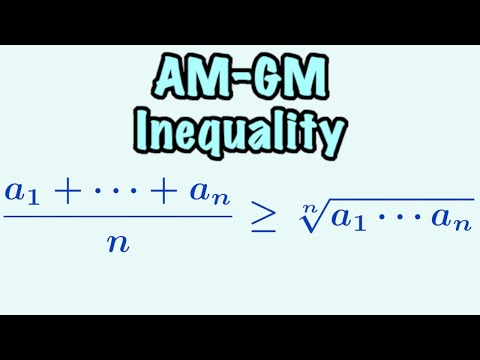 0:12:45
0:12:45
 0:04:11
0:04:11
 0:02:52
0:02:52
 0:05:11
0:05:11
 0:05:42
0:05:42
 0:19:35
0:19:35
 0:21:48
0:21:48
 0:00:55
0:00:55
 0:09:00
0:09:00
 0:08:39
0:08:39
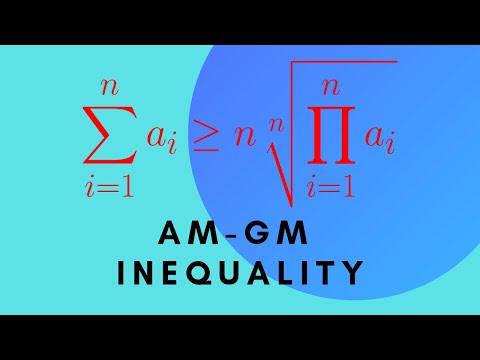 0:32:05
0:32:05
 0:49:47
0:49:47
 0:00:44
0:00:44
 0:51:31
0:51:31
 0:08:55
0:08:55
 0:04:01
0:04:01