filmov
tv
How Does Euclid’s Algorithm Give HCF? | Use Euclid's Algorithm To Find The HCF | BYJU'S Maths

Показать описание
Euclid was a famous Mathematician. Euclid's division algorithm is a method to find the highest common factor or HCF of any two numbers by using Euclid's division lemma. HCF is the largest number which exactly divides two or more positive integers. That means, on dividing both the integers a and b the remainder is zero. The basis of the Euclidean division algorithm is Euclid’s division lemma. It states that if we divide an integer by another non-zero integer, we will get a unique integer as quotient and a unique integer as remainder. We can write the above scenario mathematically as: Dividend = (Divisor × Quotient) + Remainder. We can solve many real life life problems using this algorithm. The video explains this through an interesting real life example and step by step process.
🚀 Win a NASA trip
🎓 Up to 100% Scholarship
💸 Cash Rewards
🏆 Be an All-India Rank
#byjus #BYJUSMaths #hcfcalculator #euclidsalgorithm #findthehcf #extendedeuclideanalgorithm #useeuclid'salgorithmtofindthehcfof #euclidsalgorithm #extendedeuclideanalgorithmexample #useeuclidalgorithmtofindhcfof #euclid'salgorithmtofindhcf #euclidalgorithmtofindhcf #extendedeuclideanalgorithmwithsteps #euclideanalgorithm #euclidsalgorithmexamples #HowdoesEuclid’sAlgorithmgiveHCF #UseEuclid'salgorithmtofindtheHCF #Euclid'sDivisionAlgorithm
🚀 Win a NASA trip
🎓 Up to 100% Scholarship
💸 Cash Rewards
🏆 Be an All-India Rank
#byjus #BYJUSMaths #hcfcalculator #euclidsalgorithm #findthehcf #extendedeuclideanalgorithm #useeuclid'salgorithmtofindthehcfof #euclidsalgorithm #extendedeuclideanalgorithmexample #useeuclidalgorithmtofindhcfof #euclid'salgorithmtofindhcf #euclidalgorithmtofindhcf #extendedeuclideanalgorithmwithsteps #euclideanalgorithm #euclidsalgorithmexamples #HowdoesEuclid’sAlgorithmgiveHCF #UseEuclid'salgorithmtofindtheHCF #Euclid'sDivisionAlgorithm
Комментарии
 0:00:20
0:00:20
 0:04:26
0:04:26
 0:13:29
0:13:29
 0:05:50
0:05:50
 0:11:48
0:11:48
 0:14:38
0:14:38
 0:09:30
0:09:30
 0:18:26
0:18:26
 0:08:50
0:08:50
 0:02:42
0:02:42
 0:08:31
0:08:31
 0:09:35
0:09:35
 0:04:10
0:04:10
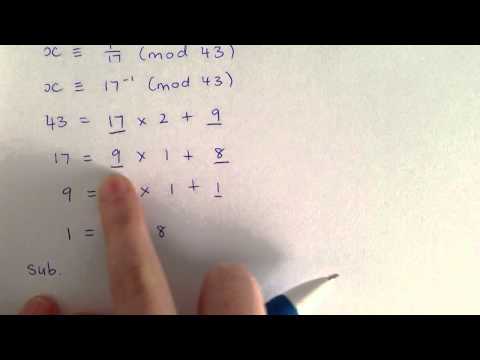 0:06:00
0:06:00
 0:00:43
0:00:43
 0:05:15
0:05:15
 0:18:20
0:18:20
 0:14:50
0:14:50
 0:06:27
0:06:27
 0:13:15
0:13:15
 0:10:16
0:10:16
 0:03:10
0:03:10
 0:06:58
0:06:58
 0:09:03
0:09:03