filmov
tv
Extended Euclidean Algorithm and Inverse Modulo Tutorial

Показать описание
Using EA and EEA to solve inverse mod.
Extended Euclidean Algorithm and Inverse Modulo Tutorial
Extended Euclidean Algorithm (Solved Example 1)
How To Find The Inverse of a Number ( mod n ) - Inverses of Modular Arithmetic - Example
Multiplicative Inverse
The Extended Euclidean algorithm
GCD, Bezout, and Modular Inverses | The Extended Euclidean Algorithm
Extended Euclidean Algorithm Example
Extended Euclidean Algorithm (Solved Example 3)
Extended Euclidean Algorithm (Solved Example 2)
Extended Euclidean Algorithm using Example Multiplicative inverse of a number | Cryptography
Finding the Multiplicative Inverse using Extended Euclidean Algorithm Example 1 HD
Inverse Modulo by Extended Euclidean Algorithm
Extended Euclidean Algorithm - Example (Simplified)
Extended Euclidean Algorithm to find the Inverse Example 1 - Part 2
The Extended Euclidean Algorithm | Inverse Modulo | Tutorial | Cryptography
Abstract Algebra | Writing a polynomial gcd as a combination -- example.
Extended Euclidean Algorithm Explained
The extended Euclidean algorithm in one simple idea
Extended Euclidean Algorithm to find Multiplicative Inverse explained with examples in Cryptography
Extended Euclidean Algorithm to find the Inverse Example 1 - Part 1
Multiplicative Inverse in cryptography
GCD and Modular Inverse: Extended Euclidean Algorithm - Part 1
Number Theory | Extended Euclidean Algorithm Example #1
Extended Euclidean Algorithm
Комментарии
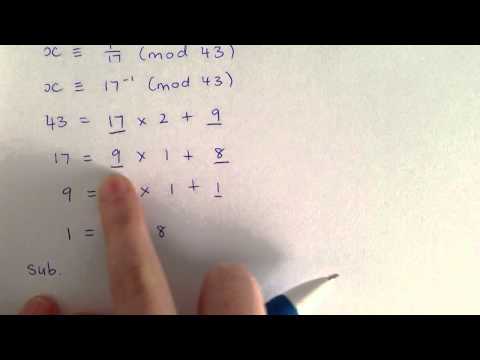 0:06:00
0:06:00
 0:10:16
0:10:16
 0:10:58
0:10:58
 0:10:03
0:10:03
 0:12:11
0:12:11
 0:22:21
0:22:21
 0:14:50
0:14:50
 0:06:54
0:06:54
 0:05:43
0:05:43
 0:04:24
0:04:24
 0:12:16
0:12:16
 0:10:26
0:10:26
 0:07:40
0:07:40
 0:09:02
0:09:02
 0:05:26
0:05:26
 0:19:48
0:19:48
 0:06:21
0:06:21
 0:10:59
0:10:59
 0:08:52
0:08:52
 0:09:12
0:09:12
 0:06:38
0:06:38
 0:44:48
0:44:48
 0:08:53
0:08:53
 0:02:42
0:02:42