filmov
tv
The Euclidean Algorithm: How and Why, Visually

Показать описание
We explain the Euclidean algorithm to compute the gcd, using visual intuition. You'll never forget it once you see the how and why. Then we write it out formally and do an example.
This is part of a playlist on GCDs and the Euclidean algorithm:
This is part of a playlist on GCDs and the Euclidean algorithm:
The Euclidean Algorithm: How and Why, Visually
Euclidean Algorithm - An example ← Number Theory
How to Find the Greatest Common Divisor by Using the Euclidian Algorithm
Number Theory: The Euclidean Algorithm Proof
EUCLIDEAN ALGORITHM - DISCRETE MATHEMATICS
The Euclidean Algorithm
GCD - Euclidean Algorithm (Method 1)
Discrete Math - 4.3.3 The Euclidean Algorithm
Euclidean algorithm to find GCD of two number
How Does Euclid’s Algorithm Give HCF? | Use Euclid's Algorithm To Find The HCF | BYJU'S Ma...
The Extended Euclidean algorithm
Why Does the Euclidean Algorithm Work? : Lessons in Applied Mathematics
Euclidean Algorithm (Proof)
How to prove the Euclid's Algorithm - GCD
Proof of the Euclidean algorithm
Extended Euclidean Algorithm and Inverse Modulo Tutorial
Number Theory: The Euclidean Algorithm Example 1
Euclidean/ Euclid's algorithm in Cryptography and network security
MAT 112: The Euclidean Algorithm
Proof of Euclidean Algorithm
Extended Euclidean Algorithm Example
Euclidean Algorithm (Made simple!)
GCD - Euclidean Algorithm (Method 2)
Extended Euclidean Algorithm
Комментарии
 0:13:29
0:13:29
 0:02:04
0:02:04
 0:04:10
0:04:10
 0:05:50
0:05:50
 0:10:02
0:10:02
 0:06:58
0:06:58
 0:14:38
0:14:38
 0:07:34
0:07:34
 0:05:15
0:05:15
 0:04:26
0:04:26
 0:12:11
0:12:11
 0:01:35
0:01:35
 0:08:50
0:08:50
 0:07:15
0:07:15
 0:10:19
0:10:19
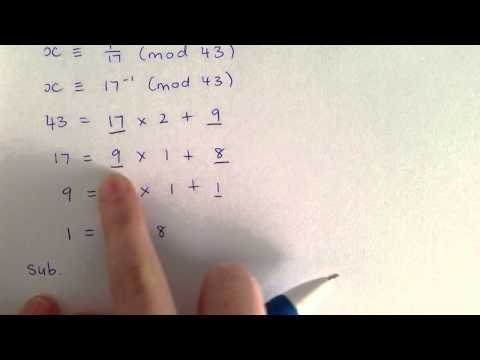 0:06:00
0:06:00
 0:02:44
0:02:44
 0:07:28
0:07:28
 0:04:44
0:04:44
 0:06:25
0:06:25
 0:14:50
0:14:50
 0:04:25
0:04:25
 0:10:00
0:10:00
 0:02:42
0:02:42